题目内容
20.已知$\sqrt{m-2}$+|n+3|=0,那么(m+n)2015的值为( )| A. | -1 | B. | 1 | C. | 52017 | D. | -52017 |
分析 根据二次根式、绝对值的非负性即可求出m与n的值.
解答 解:由题意可知:m-2=0,n+3=0,
∴m=2,n=-3,
∴m+n=-1
∴(m+n)2015=-1
故选(A)
点评 本题考查代数式求值,解题的关键是根据非负性求出m与n的值,本题属于基础题型.

练习册系列答案
相关题目
11.满足-$\sqrt{7}$<x<$\sqrt{19}$的所有整数x的和是( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
5. 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
10.若-1<x<0,则x,x2,x3的大小关系是( )
| A. | x<x3<x2 | B. | x<x2<x3 | C. | x3<x<x2 | D. | x2<x3<x |
 如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形,若AB=3,则BC=6.
如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形,若AB=3,则BC=6.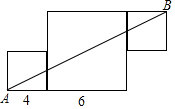 如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.
如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.