题目内容
8.在平面直角坐标系中,已知两点A(-2,0),B(4,0),点P(m,n)在一次函数y=$\frac{1}{2}$x+2的图象上,若∠APB=90°,则|m|=$\frac{4\sqrt{5}}{5}$.分析 由点P在一次函数图象上,可用m表示出n,再由点的坐标可分别表示出AB、AP、BP的长度,再根据勾股定理可得到关于m的方程,求解即可.
解答 解:
∵点P(m,n)在一次函数y=$\frac{1}{2}$x+2的图象上,
∴n=$\frac{1}{2}$m+2,
∵A(-2,0),B(4,0),P(m,$\frac{1}{2}$m+2),
∴AB2=|4-(-2)|2=36,AP2=(m+2)2+($\frac{1}{2}$m+2)2,BP2=(m-4)2+($\frac{1}{2}$m+2)2,
∵∠APB=90°,
∴AP2+BP2=AB2,即(m+2)2+($\frac{1}{2}$m+2)2+(m-4)2+($\frac{1}{2}$m+2)2=36,
解得m=±$\frac{4\sqrt{5}}{5}$,
∴|m|=$\frac{4\sqrt{5}}{5}$,
故答案为:$\frac{4\sqrt{5}}{5}$.
点评 本题主要考查一次函数图象上点的坐标特征和勾股定理,利用点的坐标分别表示出△ABP各边的长是解题的关键,注意勾股定理的应用.

练习册系列答案
相关题目
19. 如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
 如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )| A. | 2:3 | B. | 3:4 | C. | 1:1 | D. | 4:3 |
16.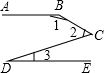 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )
 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=180° | C. | ∠1=∠2+∠3 | D. | ∠1-∠2+∠3=180° |
3.下列命题中,属于定义的是( )
| A. | 两点确定一条直线 | |
| B. | 两直线平行,内错角相等 | |
| C. | 点到直线的距离是该点到这条直线的垂线段的长度 | |
| D. | 同角或等角的余角相等 |
13.若2m2-3m-7=0,7n2+3n-2=0,其中m,n为实数,且mn≠1,则m+$\frac{1}{n}$=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
20.零是( )
| A. | 最小的正数 | B. | 最小的整数 | C. | 最大的负数 | D. | 绝对值最小的数 |
 如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.
如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG. 如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.