题目内容
8.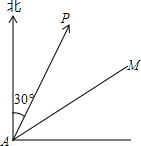 如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?
如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?
分析 作PB⊥AM于M,求出PB的长即可判断是否触礁,作⊙P的切线AE,切点为E,利用三角函数即可求出∠PAE,进而得到渔船在A处应再向北偏东至少偏离多大角度才能脱险.
解答 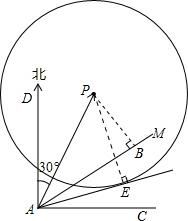 解:如图,作PB⊥AM于M.
解:如图,作PB⊥AM于M.
∵∠DAB=60°,∠DAP=30°,
∴∠PAB=60°-30°=30°,
∴PB=AP•sin30°=20海里<20$\sqrt{2}$(海里),
∴该渔船若不改变航向,有触礁的可能;
作⊙P的切线AE,切点为E.
∴sin∠PAE=$\frac{20\sqrt{2}}{40}$=$\frac{\sqrt{2}}{2}$,
∴∠PAE=45°,
∴∠DAE=30°+45°=75°,∠MAE=75°-60°=15°.
答:有可能触礁,该渔船在A处应再向北偏东至少偏离15°才能脱离危险.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,根据题意准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
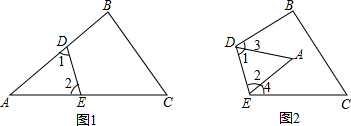

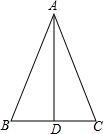 如图,在△ABC中,AB=AC,AD是边BC上的高,求证:
如图,在△ABC中,AB=AC,AD是边BC上的高,求证: 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.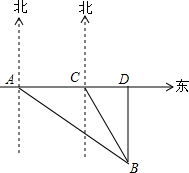 如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)