题目内容
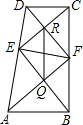 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AD=DC+AB,DE=DC,F为BC中点.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AD=DC+AB,DE=DC,F为BC中点.
(1)证明:①∠CEB=90°,②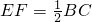 ;
;
(2)除几何性质①、②外,你还能发现哪些几何性质?请你选择其中两条进行证明.
(1)证明:①∵AB∥CD,
∴∠ADC+∠BAD=180°.
∵AD=DC+AB,DE=DC,
∴∠DCE=∠CED,AE=AB,
∴∠ABE=∠AEB,
∴∠AEB+∠CED=90°,
∴∠CEB=90°;
②∵∠CEB=90°,CF=BF,
∴EF= BC.
BC.
(2)解:其它主要结论还有:∠DFA=90°;S△AFD= S梯形ABCD等.
S梯形ABCD等.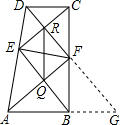
证明如下:延长DF、AB交于点G.
∵AB∥CD,
∴∠DCF=∠BGF.
又CF=BF,∠BFG=∠CFD,
∴△BFG≌△CFD,
∴BG=CD,DF=GF.
又AD=DC+AB,
∴AD=AG.
∴∠DFA=90°,S△AFD= S梯形ABCD.
S梯形ABCD.
分析:(1)①根据AB∥CD,得∠ADC+∠BAD=180°,根据AD=DC+AB,DE=DC,得∠DCE=∠CED,AE=AB,则∠ABE=∠AEB,结合三角形的内角和定理,得∠AEB+∠CED=90°,从而证明∠CEB=90°;
②根据直角三角形斜边上的中线等于斜边的一半即可证明EF= BC;
BC;
(2)利用全等三角形的性质和等腰三角形的性质可以发现:∠DFA=90°;S△AFD= S梯形ABCD等.
S梯形ABCD等.
点评:此题综合运用了等腰三角形的性质、梯形的性质、全等三角形的判定及性质.
∴∠ADC+∠BAD=180°.
∵AD=DC+AB,DE=DC,
∴∠DCE=∠CED,AE=AB,
∴∠ABE=∠AEB,
∴∠AEB+∠CED=90°,
∴∠CEB=90°;
②∵∠CEB=90°,CF=BF,
∴EF=
 BC.
BC.(2)解:其它主要结论还有:∠DFA=90°;S△AFD=
 S梯形ABCD等.
S梯形ABCD等.
证明如下:延长DF、AB交于点G.
∵AB∥CD,
∴∠DCF=∠BGF.
又CF=BF,∠BFG=∠CFD,
∴△BFG≌△CFD,
∴BG=CD,DF=GF.
又AD=DC+AB,
∴AD=AG.
∴∠DFA=90°,S△AFD=
 S梯形ABCD.
S梯形ABCD.分析:(1)①根据AB∥CD,得∠ADC+∠BAD=180°,根据AD=DC+AB,DE=DC,得∠DCE=∠CED,AE=AB,则∠ABE=∠AEB,结合三角形的内角和定理,得∠AEB+∠CED=90°,从而证明∠CEB=90°;
②根据直角三角形斜边上的中线等于斜边的一半即可证明EF=
 BC;
BC;(2)利用全等三角形的性质和等腰三角形的性质可以发现:∠DFA=90°;S△AFD=
 S梯形ABCD等.
S梯形ABCD等.点评:此题综合运用了等腰三角形的性质、梯形的性质、全等三角形的判定及性质.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.