题目内容
函数y=ax2-(a-3)x+1的图象与x轴只有一个交点,那么a的值和交点坐标分别为 .
【答案】分析:先根据函数y=ax2-(a-3)x+1的图象与x轴只有一个交点可知△=0,或者是a=0,变为一次函数,求出a的值,再由坐标轴上坐标的特点求出函数图象与坐标轴的交点即可.
解答:解:①当a=0时,函数关系式变为:y=3x+1,交点坐标为:(- ,0);
,0);
②∵函数y=ax2-(a-3)x+1的图象与x轴只有一个交点,
∴△=(a-3)2-4a=0,解得a=1或a=9.
∵当a=1时,函数y=ax2-(a-3)x+1可化为y=x2-2x+1
∴当y=0时,x=1,
∴函数与x轴交点的坐标为(1,0);
∵当a=9时,函数y=ax2-(a-3)x+1可化为y=9x2-6x+1,
∴当y=0时,x= ,
,
∴函数与x轴交点的坐标为( ,0).
,0).
故答案为:(- ,0),(1,0)、(
,0),(1,0)、( ,0).
,0).
点评:本题考查的是二次函数的图象与x轴的交点问题,熟知坐标轴上点的坐标特点是解答此题的关键.
解答:解:①当a=0时,函数关系式变为:y=3x+1,交点坐标为:(-
 ,0);
,0);②∵函数y=ax2-(a-3)x+1的图象与x轴只有一个交点,
∴△=(a-3)2-4a=0,解得a=1或a=9.
∵当a=1时,函数y=ax2-(a-3)x+1可化为y=x2-2x+1
∴当y=0时,x=1,
∴函数与x轴交点的坐标为(1,0);
∵当a=9时,函数y=ax2-(a-3)x+1可化为y=9x2-6x+1,
∴当y=0时,x=
 ,
,∴函数与x轴交点的坐标为(
 ,0).
,0).故答案为:(-
 ,0),(1,0)、(
,0),(1,0)、( ,0).
,0).点评:本题考查的是二次函数的图象与x轴的交点问题,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 15、函数y=ax2+bx+c的图象如图所示,且线段OM与ON相等,则a,b,c之间的关系为
15、函数y=ax2+bx+c的图象如图所示,且线段OM与ON相等,则a,b,c之间的关系为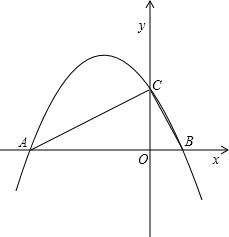 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°, 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 已知正比例函数y=ax与反比例函数
已知正比例函数y=ax与反比例函数