题目内容
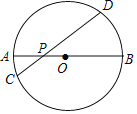
【题目】已知如图,二次函数![]() 的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.
的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.

(1)求B点的坐标及二次函数的解析式;
(2)抛物线上一点Q(m,m+3),(m为整数),点M为△ABC的外接圆上一动点,求线段QM长度的范围;
(3)将△AOC绕平面内一点P旋转180°至△A'O'C'(点O'与O为对应点),使得该三角形的对应点中的两个点落在![]() 的图象上,求出旋转中心P的坐标.
的图象上,求出旋转中心P的坐标.
【答案】(1)(4,0);![]() ;(2)
;(2)![]() ≤QM≤
≤QM≤![]() ;(3)
;(3)![]() 、
、![]()
【解析】
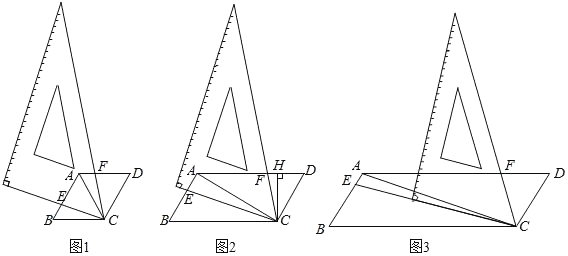
(1)过点A作AD⊥y轴于点D,AE⊥x轴于点E,求证△ACD≌△ABE,进而求得点B坐标,再将A、B两点坐标代入二次函数解析式,即可解答;
(2)将点Q(m,m+3)代入二次函数解析式,求得m的值,进而且得点Q坐标,根据圆的性质得到BC是圆N的直径,利用勾股定理即可求得BC,进而求得N的坐标,再利用勾股定理求得QN的长,确定取值范围即可;
(3)分两种情况:当点A的对称点![]() ,点O的对称点
,点O的对称点![]() 在抛物线上时,利用旋转180°可知,
在抛物线上时,利用旋转180°可知,![]() ∥
∥![]() ,设点
,设点![]() 的横坐标为m,则点
的横坐标为m,则点![]() 的横坐标为m-3,利用
的横坐标为m-3,利用![]() 列出式子,即可求得m的值,利用旋转中心和线段中点的特点,即可求得旋转中心P的坐标;当点A的对称点
列出式子,即可求得m的值,利用旋转中心和线段中点的特点,即可求得旋转中心P的坐标;当点A的对称点![]() ,点C的对称点
,点C的对称点![]() 在抛物线上时,设点
在抛物线上时,设点![]() 的横坐标为m,则点
的横坐标为m,则点![]() 的横坐标为m-3,同理可求得m的值以及旋转中心P的坐标.
的横坐标为m-3,同理可求得m的值以及旋转中心P的坐标.
(1)解:如图,过点A作AD⊥y轴于点D,AE⊥x轴于点E,
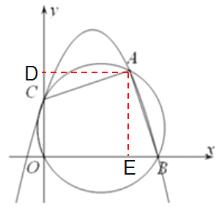
∴∠ADC=∠AEB=90°
∵二次函数![]() 与y轴交于点C,
与y轴交于点C,
点C坐标为(0,2)
∵点A坐标(3,3)
∴DA=AE=3
∵∠DAC+∠CAE=90°
∠EAB+∠CAE=90°
∴∠DAC=∠EAB
∴△ACD≌△ABE
∴EB=CD=3-2=1
OB=3+1=4
∴点B的坐标为(4,0)
将A(3,3)B(4,0)代入二次函数![]() 中
中
得:![]()
解得: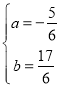
二次函数的解析式为:![]()
(2)将点Q(m,m+3)代入二次函数解析式得:![]()
m1=1;m2=![]() (舍)
(舍)
∴m=1
∴点Q坐标为(1,4)
由勾股定理得:BC=2![]()
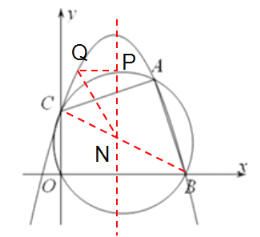
设圆的圆心为N
∵圆经过点O,且∠COB=90°
∴BC是圆N的直径,
∴圆N的半径为![]() ,N的坐标为(2,1)
,N的坐标为(2,1)
由勾股定理得,QN=![]()
半径r=![]() ,则
,则![]() ≤QM≤
≤QM≤![]()
(3)当点A的对称点![]() ,点O的对称点
,点O的对称点![]() 在抛物线上时,如图
在抛物线上时,如图
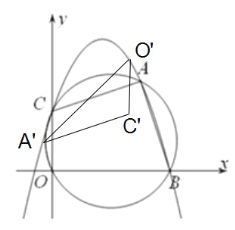
设点![]() 的横坐标为m,则点
的横坐标为m,则点![]() 的横坐标为m-3
的横坐标为m-3
![]()
得:![]()
解得:![]()
∴![]() 的坐标为(
的坐标为(![]() )
)
∴旋转中心P的坐标为![]()
当点A的对称点![]() ,点C的对称点
,点C的对称点![]() 在抛物线上时,如图
在抛物线上时,如图
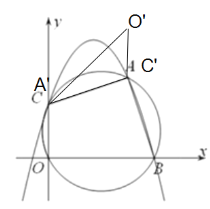
设点![]() 的横坐标为m,则点
的横坐标为m,则点![]() 的横坐标为m-3
的横坐标为m-3
![]()
得:![]()
解得:![]()
∴![]() 的坐标为(
的坐标为(![]() )
)
∴旋转中心P的坐标为![]()
综上所述,旋转中心P的坐标为![]() 或
或![]()

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】有这样一个问题,探究函数y=x2﹣2![]() 的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2
的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2![]() 的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2![]() 的自变量取值范围是 .
的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | |
y | … | n | 3 | 0 | ﹣1 | 0 | ﹣1 | 0 | 3 | m |
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;
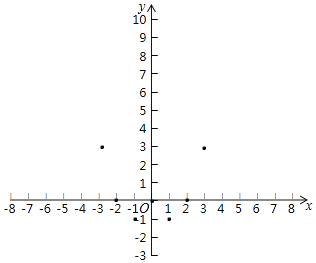
(4)进一步探究发现,该函数图象在第四象限内的最低点是1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);
(5)根据图象回答:方程x2﹣2![]() =﹣
=﹣![]() 有 个实数解.
有 个实数解.