题目内容
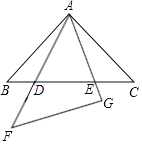
【题目】如图,![]() ,点
,点![]() 是线段
是线段![]() 的一个三等分点,以点
的一个三等分点,以点![]() 为圆心,
为圆心,![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
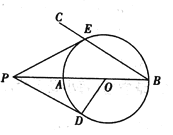
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 上的一动点,连接
上的一动点,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
【答案】(1)见解析;(2)①60°,②120°.
【解析】
(1)连接![]() ,由
,由![]() ,得到
,得到![]() 为等边三角形,得到
为等边三角形,得到![]() ,即可得到
,即可得到![]() ,则结论成立;
,则结论成立;
(2)①连接BD,由圆周角定理,得到∠ABD=30°,则∠DBE=60°,又有∠BEP=120°,根据同旁内角互补得到PE//DB,然后证明![]() ,即可得到答案;
,即可得到答案;
②由圆周角定理,得∠ABD=60°,得到∠EBD=90°,然后由直径所对的圆周角为90°,得到![]() ,即可得到答案.
,即可得到答案.
证明:连接![]() ,
,
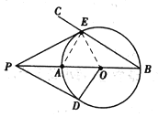
![]() ,
,
![]() .
.
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() .
.
![]() 点
点![]() 是
是![]() 的三等分点,
的三等分点,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 是
是![]() 的切线.
的切线.
(2)①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
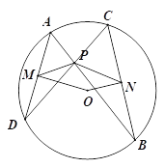
如图,连接BD,
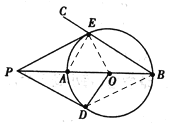
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB为直径,则∠AEB=90°,
由(1)知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴PE//DB,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
故答案为:60°.
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
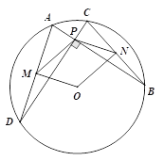
如图,连接AE、AD、DB,
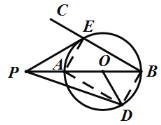
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB是直径,
∴![]() ,
,
∴四边形![]() 是矩形.
是矩形.
故答案为:![]() .
.

练习册系列答案
相关题目