Question

【题目】在同一平面内，将两个全等的等腰直角三角形和摆放在一起，为公共顶点，，若固定不动，绕点旋转，、与边的交点分别为、（点不与点重合，点不与点重合）．

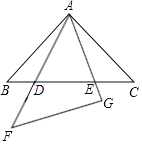
（1）求证：；

（2）在旋转过程中，试判断等式是否始终成立，若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）详见解析；（2）成立．

【解析】

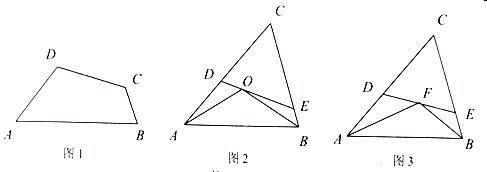
（1）由图形得∠BAE=∠BAD+45°，由外角定理，得∠CDA=∠BAD+45°，可得∠BAE=∠CDA，根据∠B=∠C=45°，证明两个三角形相似；
（2）将△ACE绕点A顺时针旋转90°至△ABH位置，证明△EAD≌△HAD转化DE、EC，使所求线段集中在Rt△BHD中利用勾股定理解决．

（1）∵∠BAE=∠BAD+45°，∠CDA=∠BAD+45°，
∴∠BAE=∠CDA，
又∠B=∠C=45°，
∴△ABE∽△DCA；
（2）成立．如图，将△ACE绕点A顺时针旋转90°至△ABH位置，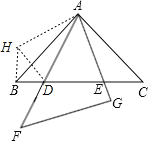

则CE=BH，AE=AH，∠ABH=∠C=45°，旋转角∠EAH=90°．
连接HD，在△EAD和△HAD中，

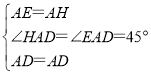
∴△EAD≌△HAD（SAS）．
∴DH=DE．
又∠HBD=∠ABH+∠ABD=90°，
∴BD2+BH2=HD2，即BD2+CE2=DE2．