题目内容
已知三个关于y的方程:y2-y+a=0,(a-1)y2+2y+1=0和(a-2)y2+2y-1=0,若其中至少有两个方程有实根,则实数a的取值范围是 .
考点:根的判别式
专题:计算题
分析:分别找出方程有解时a的范围,求出至少有两个方程有实根时实数a的取值范围即可.
解答:解:关于y的方程:y2-y+a=0有解,即△=1-4a≥0,即a≤
;
方程(a-1)y2+2y+1=0,
当a=1时,方程有解;
当a≠1时,△=4-4(a-1)≥0,即a≤2,
此时a的范围为a≤2且a≠1;
方程(a-2)y2+2y-1=0,
当a=2时,方程有解;
当a≠2时,△=4+4(a-2)≥0,即a≥1,
此时a的范围为a≥1,
综上,a的范围为a≤
或1<a≤2.
故答案为:a≤
或1<a≤2
| 1 |
| 4 |
方程(a-1)y2+2y+1=0,
当a=1时,方程有解;
当a≠1时,△=4-4(a-1)≥0,即a≤2,
此时a的范围为a≤2且a≠1;
方程(a-2)y2+2y-1=0,
当a=2时,方程有解;
当a≠2时,△=4+4(a-2)≥0,即a≥1,
此时a的范围为a≥1,
综上,a的范围为a≤
| 1 |
| 4 |
故答案为:a≤
| 1 |
| 4 |
点评:此题考查了根的判别式,熟练掌握根的判别式的意义是解本题的关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列方程中是关于x的一元二次方程的是( )
A、x2+
| ||
B、
| ||
| C、(x-1)(x+2)=1 | ||
| D、3x2-2xy-5y2=0 |
 已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有
已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有 如图,将两根等宽的纸条叠放在一起,重叠的部分(图中阴影部分)是一个四边形,对这个四边形的形状,你认为最准确的描述是:这个四边形是一个
如图,将两根等宽的纸条叠放在一起,重叠的部分(图中阴影部分)是一个四边形,对这个四边形的形状,你认为最准确的描述是:这个四边形是一个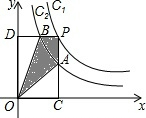 如图,两个反比例函数y1=
如图,两个反比例函数y1=