题目内容
7.解不等式(组):(1)5x-6≤2(x+3)
(2)$\frac{2x-1}{2}$-$\frac{5x-1}{4}$<0
(3)解不等式组:$\left\{\begin{array}{l}{9x+5<8x+7}\\{\frac{4}{3}x+2>1-\frac{3}{2}x}\end{array}\right.$,并把解集在数轴上表示出来.
(4)解不等式组$\left\{\begin{array}{l}{3(x-1)<5x+1}\\{\frac{x-1}{2}≥2x-4}\end{array}\right.$,并指出它的所有的非负整数解.
分析 (1)不等式去括号,移项合并,把x系数化为1,即可求出解集;
(2)不等式去分母,去括号,移项合并,把x系数化为1,即可求出解集;
(3)分别求出不等式组中两不等式的解集,找出两解集的公共部分,确定出不等式组的解集,表示在数轴上即可;
(4)分别求出不等式组中两不等式的解集,找出两解集的公共部分,确定出不等式组的解集,进而求出所有的非负整数解即可.
解答 解:(1)去括号得:5x-6≤2x+6,
移项合并得:3x≤12,
解得:x≤4;
(2)去分母得:4x-2-5x+1<0,
移项合并得:-x<1,
解得:x>-1;
(3)$\left\{\begin{array}{l}{9x+5<8x+7①}\\{\frac{4}{3}x+2>1-\frac{3}{2}x②}\end{array}\right.$,
由①得:x<2,
由②得:x>-$\frac{2}{5}$,
则不等式组的解集为-$\frac{2}{5}$<x<2;
(4)$\left\{\begin{array}{l}{3(x-1)<5x+1①}\\{\frac{x-1}{2}≥2x-4②}\end{array}\right.$,
由①得:x>-2,
由②得:x≤$\frac{7}{3}$,
则不等式组的解集为-2<x≤$\frac{7}{3}$,即所有非负整数解为0,1,2.
点评 此题考查了一元一次不等式组的整数解,以及在数轴上表示不等式的解集,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
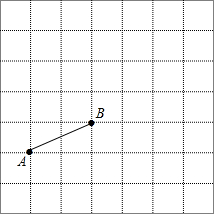 如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.
如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.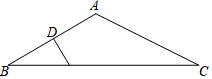 如图,△ABC中,AB=AC,且∠BAC=108°,点D是AB上一定点,请在BC边上找一点E,使以B、D、E为顶点的三角形与△ABC相似.
如图,△ABC中,AB=AC,且∠BAC=108°,点D是AB上一定点,请在BC边上找一点E,使以B、D、E为顶点的三角形与△ABC相似. 如图,当∠1=∠2时,直线a、b平行吗,为什么?
如图,当∠1=∠2时,直线a、b平行吗,为什么?