题目内容
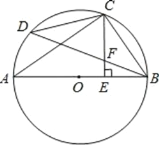
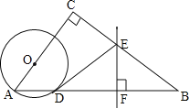
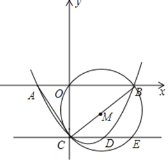
【题目】如图,抛物线![]() 与x轴相交于点A(-2,0)、B(4,0),与y轴相交于点C,连接BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E.
与x轴相交于点A(-2,0)、B(4,0),与y轴相交于点C,连接BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E.
(1)求该抛物线所对应的函数关系式;
(2)求线段DE的长;
(3)在BC下方的抛物线上有一点P,P点的横坐标是m,△PBC的面积为S,求出S与m之间的函数关系式,并求出当m为何值时,S有最大值,最大值为多少?
【答案】(1)![]() ;(2)2;(3)
;(2)2;(3)![]() ,当m=2时,S有最大值
,当m=2时,S有最大值
最大值为3.
【解析】
(1)根据点A、B的坐标,利用待定系数法即可求出抛物线所对应的函数关系式;
(2)连接BE,则四边形OCEB为矩形,根据矩形的性质可知CE的长度,由抛物线与x轴交于点A、B可找出抛物线的对称轴,结合点C在y轴上即可求出CD的长度,再利用DE=CE-CD即可求出结论;
(3)过点P作PH⊥x轴于点H,由点P的横坐标可得出点P、H的坐标,进而可得出OH、PH、BH的长度,由抛物线所对应的函数关系式利用二次函数图象上点的坐标特征可求出点C的坐标,进而可得出OC的长度,由S=S梯形OCPH+S△BPH-S△BOC可找出S与m之间的函数关系式,再利用配方法即可解决最值问题.
(1)将A(2,0)、B(4,0)代入函数解析式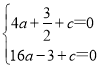 ,
,
解得: ,
,
∴该抛物线所对应的函数关系式为![]()
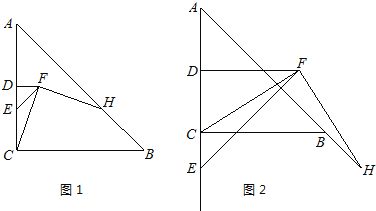
(2)连接BE,如图1所示.
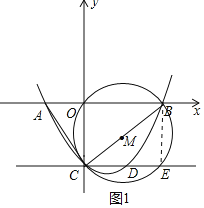
∵线段BC为⊙M的直径,
∴∠BEC=90°.
又∵CE∥AB,∠BOC=∠OCE=90°,
∴四边形OCEB为矩形,
∴CE=OB=4.
∵抛物线y=![]() x2-
x2-![]() x-3与x轴相交于点A(-2,0)、B(4,0),
x-3与x轴相交于点A(-2,0)、B(4,0),
∴抛物线的对称轴为直线x=1,
又∵点C在y轴上,
∴CD=1×2=2,
∴DE=CE-CD=2.
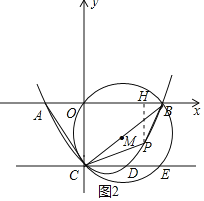
(3)过点P作PH⊥x轴于点H,如图2所示.
∵P点的横坐标是m,点在BC下方的抛物线上,
∴点P的坐标为(m,![]() m2-
m2-![]() m-3)(0<m<4),点H的坐标为(m,0),
m-3)(0<m<4),点H的坐标为(m,0),
∴OH=m,BH=4-m,PH=-![]() m2+
m2+![]() m+3.
m+3.
∵抛物线y=![]() x2-
x2-![]() x-3与y轴相交于点C,∴点C的坐标为(0,-3),
x-3与y轴相交于点C,∴点C的坐标为(0,-3),
∴OC=3,
∴S=S梯形OCPH+S△BPH-S△BOC,
=![]() (OC+PH)OH+
(OC+PH)OH+![]() BHPH-
BHPH-![]() OBOC,
OBOC,
=![]() ×(3-
×(3-![]() m2+
m2+![]() m+3)×m+
m+3)×m+![]() ×(4-m)×(-
×(4-m)×(-![]() m2+
m2+![]() m+3)-
m+3)-![]() ×4×3,
×4×3,
=-![]() m2+3m=-
m2+3m=-![]() (m-2)2+3,
(m-2)2+3,
∵-![]() <0,
<0,
∴当m=2时,S有最大值,最大值为3.
综上所述:S与m之间的函数关系式为S=-![]() m2+3m(0<m<4),当m=2时,S有最大值,最大值为3.
m2+3m(0<m<4),当m=2时,S有最大值,最大值为3.