题目内容
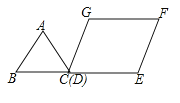
【题目】如图,等边![]() 边长为2,四边形
边长为2,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 和
和![]() 在同一条直线上,且点
在同一条直线上,且点![]() 与点
与点![]() 重合,现将
重合,现将![]() 沿
沿![]() 的方向以每秒1个单位的速度匀速运动,当点
的方向以每秒1个单位的速度匀速运动,当点![]() 与点
与点![]() 重合时停止,则在这个运动过程中,
重合时停止,则在这个运动过程中,![]() 与四边形
与四边形![]() 的重合部分的面积
的重合部分的面积![]() 与运动时间
与运动时间![]() 之间的函数关系图象大致是( )
之间的函数关系图象大致是( )
A. B.
B.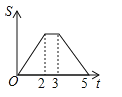 C.
C.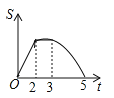 D.
D.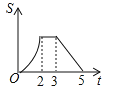
【答案】A
【解析】
分三种情况:①0≤t≤2时,由重叠部分为边长为t的等边三角形可得S=![]() t2;②2<t≤3时,由重叠部分即为△ABC得S=
t2;②2<t≤3时,由重叠部分即为△ABC得S=![]() ×22=
×22=![]() ;③3<t≤5时由重叠部分是S△ABC-S△HEC且△HEC边长为t-3可得S=-
;③3<t≤5时由重叠部分是S△ABC-S△HEC且△HEC边长为t-3可得S=-![]() t2+
t2+![]() ,据此可得答案.
,据此可得答案.
①当0≤t≤2时,如图1,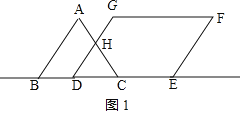
由题意知CD=t,∠HDC=∠HCD=60°,
∴△CDH是等边三角形,
则S=![]() t2;
t2;
②当2<t≤3时,如图2,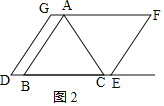
S=![]() ×22=
×22=![]() ;
;
③当3<t≤5时,如图3,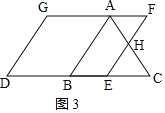
根据题意可得CE=CD-DE=t-3,∠C=∠HEC=60°,
∴△CEH为等边三角形,
则S=S△ABC-S△HEC=![]() ×22-
×22-![]() (t-3)2=-
(t-3)2=-![]() t2+
t2+![]() ;
;
综上,0≤t≤2时函数图象是开口向上的抛物线的一部分,2<t≤3时函数图象是平行于x轴的一部分,当3<t≤5时函数图象是开口向下的抛物线的一部分;
故选:A.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目