题目内容
 已知二次函数y=ax+bx+c(a≠0)的图象如图所示,以下结论中正确的个数是( )
已知二次函数y=ax+bx+c(a≠0)的图象如图所示,以下结论中正确的个数是( )①abc>0、②3a>2b、③m(am+b)≤a-b(m为任意实数)、④4a-2b+c<0.
| A、1 | B、2 | C、3 | D、4 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线开口向下得a<0,由抛物线的对称轴为直线x=-
=-1得b=2a<0,由抛物线与y轴的交点在x轴上方得c>0,所以abc>0;由b=2a,则2b-3a=a<0,所以2b<3a;根据抛物线的对称轴为直线x=-1,开口向下,得到当x=-1时,y有最大值,所以am2+bm+c≤a-b+c(m为任意实数),整理得到m(am+b)≤a-b(m为任意实数);根据抛物线的对称性得到抛物线与x轴的一个交点在点(-3,0)和(-2,0)之间,则当x=-2时,y>0,即4a-2b+c>0.
| b |
| 2a |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
=-1<0,
∴b=2a,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵b=2a,
∴3a-2b=3a-4a=-a>0,
∴3a>2b,所以②正确;
∵抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2+bm+c≤a-b+c(m为任意实数),
∴m(am+b)≤a-b(m为任意实数),所以③正确;
∵抛物线的对称轴为直线x=-1,抛物线与x轴的一个交点在点(0,0)和(1,0)之间,
∴抛物线与x轴的一个交点在点(-3,0)和(-2,0)之间,
∴当x=-2时,y>0,
∴4a-2b+c>0,所以④错误.
故选C.
∴a<0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵b=2a,
∴3a-2b=3a-4a=-a>0,
∴3a>2b,所以②正确;
∵抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2+bm+c≤a-b+c(m为任意实数),
∴m(am+b)≤a-b(m为任意实数),所以③正确;
∵抛物线的对称轴为直线x=-1,抛物线与x轴的一个交点在点(0,0)和(1,0)之间,
∴抛物线与x轴的一个交点在点(-3,0)和(-2,0)之间,
∴当x=-2时,y>0,
∴4a-2b+c>0,所以④错误.
故选C.
点评:此题主要考查了二次函数图象与系数的关系,同学们应注意,二次函数y=ax2+bx+c(a≠0)的图象,当a<0时,抛物线向下开口,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右,以及利用对称轴得出a,b的关系是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
在-3,
,0,-
四个数中,最小的数是( )
| 1 |
| 4 |
| 2 |
| A、-3 | ||
B、
| ||
| C、0 | ||
D、-
|
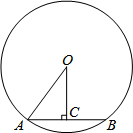 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,⊙O半径为10.
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,⊙O半径为10.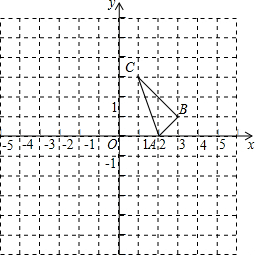 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题: