题目内容
8.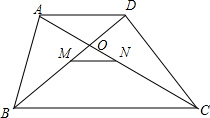 如图,在四边形ABCD中,AD∥BC,AD<BC,M,N分别是对角线BD,AC的中点,试探索MN与两底的位置关系与数量关系,并说明理由.
如图,在四边形ABCD中,AD∥BC,AD<BC,M,N分别是对角线BD,AC的中点,试探索MN与两底的位置关系与数量关系,并说明理由.
分析 连接AM并延长交BC于H,证明△AMD≌△HMB,得到AM=MH,AD=BH,根据三角形中位线定理证明结论.
解答 解: 连接AM并延长交BC于H,
连接AM并延长交BC于H,
∵AD∥BC,
∴∠ADB=∠HBD,
在△AMD和△HMB中,
$\left\{\begin{array}{l}{∠ADM=∠HBM}\\{DM=BM}\\{∠AMD=∠HMB}\end{array}\right.$,
∴△AMD≌△HMB,
∴AM=MH,AD=BH,
∵AM=MH,AN=NC,
∴MN∥HC,MN=$\frac{1}{2}$HC,
∴MN∥BC∥AD,
MN=$\frac{1}{2}$(BC-AD).
点评 本题考查了三角形中位线的性质、梯形的性质以及全等三角形的判定与性质,注意掌握辅助线的作法,灵活运用数形结合思想.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.多项式a4-3a3+9a+2与多项式3a3-a4+8-4a的和一定是( )
| A. | 偶数 | B. | 奇数 | C. | 10的倍数 | D. | 以上答案郡不对 |
10.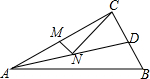 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
 如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.
如图,六边形在正方形网格内,连接六边形中两两不相邻的三个顶点,得到△AEC,说明为什么这个三角形的面积等于六边形面积的一半.