题目内容
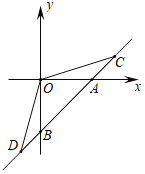
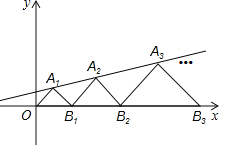
【题目】如图，在平面直角坐标系中，点
，
，
，…和
，
，
，…分别在直线
和
轴上.
，
，
，…都是等腰直角三角形，它们的面积分别记作
，
，
，…，如果点的坐标为
，那么
的纵坐标为_______.
【答案】
【解析】
因为每个A点为等腰直角三角形的直角顶点，则每个点A的纵坐标为对应等腰直角三角形的斜边一半．故先设出各点A的纵坐标，可以表示A的横坐标，代入解析式可求点A的纵坐标，规律可求．
分别过点A1，A2，A3，…向x轴作垂线，垂足为C1，C2，C3，…
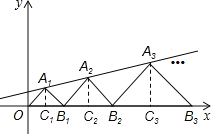
∵点A1（1，1）在直线y=
x+b上
∴代入求得：b=
∴y=x+
∵△OA1B1为等腰直角三角形
∴OB1=2
设点A2坐标为（a，b）
∵△B1A2B2为等腰直角三角形
∴A2C2=B1C2=b
∴a=OC2=OB1+B1C2=2+b
把A2（2+b，b）代入y=x+
解得b=
∴OB2=5
同理设点A3坐标为（a，b）
∵△B2A3B3为等腰直角三角形
∴A3C3=B2C3=b
∴a=OC3=OB2+B2C3=5+b
把A3（5+b，b）代入y=x+
解得b=
以此类推，发现每个A的纵坐标依次是前一个的倍
则A2019的纵坐标是()2019
故答案为：()2019
练习册系列答案
备战中考寒假系列答案
相关题目
【题目】一个水库的水位在某段时间内持续上涨，表记录了连续5小时内6个时间点的水位高度，其中
表示时间，
表示水位高度.
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 3 | 3.3 | 3.6 | 3.9 | 4.2 | 4.5 | … |
（1）通过观察数据，请写出水位高度（米）与时间（小时）的函数解析式（不需要写出定义域）；
（2）据估计，这种上涨规律还会持续，并且当水位高度达到8米时，水库报警系统会自动发出警报，请预测再过多久系统会发出警报.