题目内容
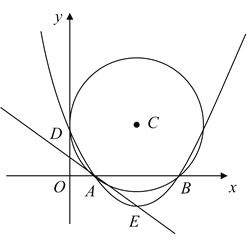
【题目】如图，已知
是圆
的直径，
是圆上一点，
的平分线交
于点
，交的切线
于点
，过点作
，交
的延长线于点
.
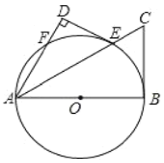
（1）求证：
是的切线；
（2）若
，
，
①求
的值；②若点
为
上一点，求
最小值.
【答案】（1）见解析；（2）①
；②
的最小值为3
【解析】
（1）根据切线的判定，连接过切点E的半径OE，利用等腰三角形和平行线性质即能证得OE⊥DE．
（2）①观察DE所在的△ADE与CE所在的△BCE的关系，由等角的余角相等易证△ADE∽△BEC，即得
的值．②先利用的值和相似求出圆的直径，发现∠BAC=30°；利用30°所对直角边等于斜边一半，给EG构造以EG为斜边且有30°的直角三角形，把
EG转化到EP，再从P出发构造PQ=OG，最终得到三点成一直线时线段和最短的模型．
（1）证明：连接
，
，
平分
，
，
，
，
，
，
，
是
的切线
（2）①连接
是直径
，
，
，
是的切线，
，
，
，
，
，
，
，
，
，
，
②过点
作
于
，过点
作
交
于
，过点作
交
于
，四边形
是平行四边形
，
.
设
，
，
，
，
，
即
解得：
，
（舍去）
，
，
，
，
，
，
，
当、、在同一直线上（即、重合）时，
最短，
，
的最小值为3.
练习册系列答案
相关题目
