题目内容
15. 如图,直角△ABC中,AB⊥AC,AD⊥BC,证明:AB2=BD•BC,AC2=CD•BC,AD2=BD•CD.
如图,直角△ABC中,AB⊥AC,AD⊥BC,证明:AB2=BD•BC,AC2=CD•BC,AD2=BD•CD.
分析 证明△ABD∽△CBA,由相似三角形的性质可知$\frac{AB}{BC}=\frac{BD}{AB}$,故此可得到:AB2=BD•BC;证明△ADC∽△BAC,由相似三角形的性质可知$\frac{AC}{BC}=\frac{DC}{AC}$故此AC2=CD•BC;证明△ABD∽△CAD,由相似三角形的性质可知$\frac{AD}{BD}=\frac{DC}{AD}$,故此可知:AD2=BD•CD.
解答 证明:在△ABD和△CBA中,
∠B=∠B,∠BAC=∠ADB=90°,
∴△ABD∽△CBA.
∴$\frac{AB}{BC}=\frac{BD}{AB}$.
∴AB2=BD•BC.
在△ADC和△BAC中,
∠C=∠C,∠BAC=∠ADC=90°,
∴△ADC∽△BAC.
∴$\frac{AC}{BC}=\frac{DC}{AC}$.
∴AC2=CD•BC.
∵.△ADC∽△BAC,△ABD∽△CBA,
∴△ABD∽△CAD.
∴$\frac{AD}{BD}=\frac{DC}{AD}$.
∴AD2=BD•CD.
点评 本题主要考查的是相似三角形的性质和判定,掌握相似三角形的性质和判定是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
5.下列数值中是不等式2x+3>9的解的是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
6.今年我市有近2万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这1000名考生是总体的一个样本 | B. | 近2万名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
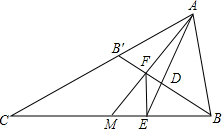 如图,已知在△ABC中,M是BC的中点,AE是∠BAC的平分线,过B作BD⊥AE,垂足为D,AM与BD相交于F,求证:EF∥AB.
如图,已知在△ABC中,M是BC的中点,AE是∠BAC的平分线,过B作BD⊥AE,垂足为D,AM与BD相交于F,求证:EF∥AB.
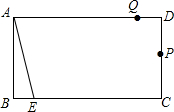 如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?
如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?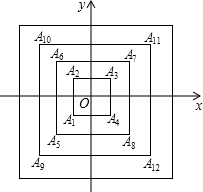 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2015的坐标是(504,504).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2015的坐标是(504,504).