Question

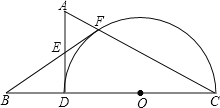
【题目】已知，如图，在△ADC中，∠ADC＝90°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED＝2∠C．

（1）求证：BF是⊙O的切线；

（2）若BF＝FC，，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）⊙O的半径是3．

【解析】

（1）欲证BF是圆O的切线，只需证明OF⊥BF；

（2）根据角与角间的数量关系推知△AEF的等边三角形．所以易求AD=2．则通过解直角△ADC来求直径CD的长度．

（1）证明：连接OF．

∵∠OFB=180°﹣∠B﹣∠BOF=180°﹣∠B﹣2∠C=180°﹣∠B﹣∠BED=90°，

∴OF⊥BF，

∴BF是⊙O的切线；

（2）解：∵BF=FC，

∴∠B=∠FCB，

∵∠BED=2∠C，

∴∠BDE+∠B=3∠C=90°，

∴∠B=∠C=30°，

∴∠AFE=60°，∠BED=60°，

∴△AEF是等边三角形，

则EF=AE=．

∴AD=2．

又∵∠C=30°，

∴CD=6，

∴⊙O的半径是3．