题目内容
1. 已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC,△BOC,△BCD的面积分别为S1,S2和S3,用等式表示S1,S2,S3之间的数量关系,并说明理由;
(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时刻直线MN的解析式;若不存在,请说明理由.
分析 (1)利用待定系数法求出抛物线的解析式,用配方法把一般式化为顶点式求出点D的坐标;
(2)根据点的坐标求出△AOC,△BOC的面积,利用勾股定理的逆定理判断△BCD为直角三角形,求出其面积,计算即可得到答案;
(3)假设存在,设点M的坐标为(m,0),表示出MA的长,根据MN∥BC,得到比例式求出AN,根据△AMN∽△ACM,得到比例式求出m,得到点M的坐标,求出BC的解析式,根据MN∥BC,设直线MN的解析式,求解即可.
解答 解: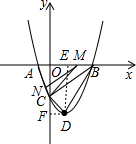 (1)∵抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,
(1)∵抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,
∴$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$.
∴抛物线的解析式为:y=x2-2x-3,
y=x2-2x-3=(x-1)2-4,
∴点D的坐标为:(1,-4);
(2)S1+S3=S2,
过点D作DE⊥x轴于点E,DF⊥y轴于F,
由题意得,CD=$\sqrt{2}$,BD=2$\sqrt{5}$,BC=3$\sqrt{2}$,
CD2+BC2=BD2,
∴△BCD是直角三角形,
S1=$\frac{1}{2}$×OA×OC=$\frac{3}{2}$,
S2=$\frac{1}{2}$×OB×OC=$\frac{9}{2}$
S3=$\frac{1}{2}$×CD×BC=3,
∴S1+S3=S2;
(3)存在点M使∠AMN=∠ACM,
设点M的坐标为(m,0),
∵-1<m<3,
∴MA=m+1,AC=$\sqrt{10}$,
∵MN∥BC,
∴$\frac{AM}{AN}$=$\frac{AB}{AC}$,即$\frac{m+1}{AN}$=$\frac{4}{\sqrt{10}}$,
解得,AN=$\frac{\sqrt{10}}{4}$(m+1),
∵∠AMN=∠ACM,∠MAN=∠CAM,
∴△AMN∽△ACM,
∴$\frac{AM}{AC}$=$\frac{AN}{AM}$,即(m+1)2=$\sqrt{10}$•$\frac{\sqrt{10}}{4}$(m+1),
解得,m1=$\frac{3}{2}$,m2=-1(舍去),
∴点M的坐标为($\frac{3}{2}$,0),
设BC的解析式为y=kx+b,把B(3,0),C(0,-3)代入得,
$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
则BC的解析式为y=x-3,又MN∥BC,
∴设直线MN的解析式为y=x+b,把点M的坐标为($\frac{3}{2}$,0)代入得,
b=-$\frac{3}{2}$,
∴直线MN的解析式为y=x-$\frac{3}{2}$.
点评 本题考查的是二次函数的解析式的确定和相似三角形的判定和性质,灵活运用待定系数法二次函数和一次函数求解析式是解题的关键,注意一元二次方程的解法和勾股定理逆定理的运用.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案老师评分统计表格:
| 评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
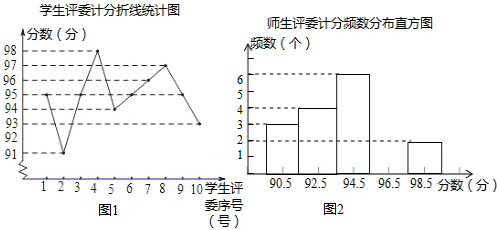
(1)在频数分布直方图中,自左向右第四组的频数为5;
(2)学生评委计分的中位数是95分;
(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,别且按老师、学生各占60%、40%的方法计算各班最后得分.已知甲班最后得分为94.4分,求统计表中x的值.
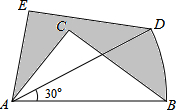 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )| A. | $\frac{25}{12}$π | B. | $\frac{4}{3}$π | C. | $\frac{3}{4}$π | D. | $\frac{5}{12}$π |
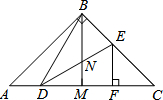 如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论: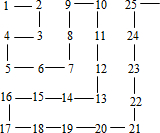 将自然数从1开始,按如图所表示的规律排列,规定图中第m行、第n列的位置记作(m,n),如自然数8的位置是(2,3),则自然数179的位置记作(10,14).
将自然数从1开始,按如图所表示的规律排列,规定图中第m行、第n列的位置记作(m,n),如自然数8的位置是(2,3),则自然数179的位置记作(10,14).