题目内容
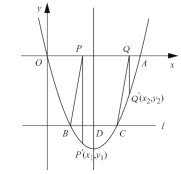
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
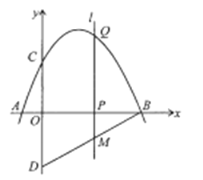
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当m=2时,即P运动到(2,0)时,△DQB面积最大,,△DQB的最大面积为24,此时Q(2,6);(3)此时点E的坐标为(5,0).
;(2)当m=2时,即P运动到(2,0)时,△DQB面积最大,,△DQB的最大面积为24,此时Q(2,6);(3)此时点E的坐标为(5,0).
【解析】
(1)把点代入解析式联立方程组即可得到结果;
(2)先求出BD所在直线的解析式![]() ,设Q(m,
,设Q(m,![]() ),M(m,
),M(m,![]() )可得,MQ
)可得,MQ![]() ,根据S△DBQ= S△DMQ +S△BMQ
,根据S△DBQ= S△DMQ +S△BMQ
可得出结果;
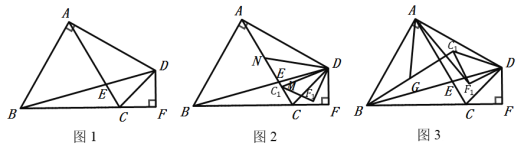
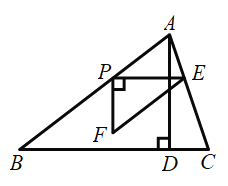
(3)过点E作EF⊥BD,垂足为F,根据当点Q、E、F在一条直线上时,![]() 有最小值即可得到结果;
有最小值即可得到结果;
(1)∵抛物线![]() 与x轴交于点A(-1,0),B(6,0),
与x轴交于点A(-1,0),B(6,0),
∴![]() ,
,
解得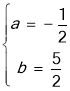 ,
,
∴抛物线的解析式![]() ,
,
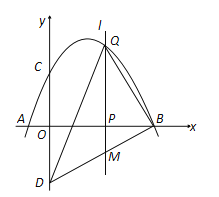
(2)令x=0,则y=3. ∴C(0,3).
∵点C与点D关于x轴对称,
∴D(0,﹣3)
设直线BD的解析式为y=kx﹣3(k≠0).
将(6,0)代入得:6k﹣3=0,
∴k=![]() .
.
∴直线BD的解析式为![]() .
.
∵直线l⊥x轴于点P,交抛物线于Q,交直线BD于点M,
且P(m,0),
∴Q(m,![]() ),M(m,
),M(m,![]() ),
),
∴MQ =![]() ,
,
![]() ,.
,.
∴S
![]()
![]()
∴当m=2时,即P运动到(2,0)时,△DQB面积最大,
此时Q(2,6),△DQB的最大值为24.
(3)在Rt△OBD中,OB=6,OD=3,则BD=![]() ,
,
∴sin∠OBD=![]() .
.
过点E作EF⊥BD,垂足为F.
Rt△BFE中,
sin∠OBD= sin∠EBF=![]() .
.
∴EF=![]() BE.
BE.
∴![]() .
.
∴当点Q、E、F在一条直线上时,![]() 有最小值.
有最小值.
∵S△DBQ ![]() ,
,
∴![]()
解得![]()
即![]() 的最小值为
的最小值为![]()
此时点E的坐标为(5,0).
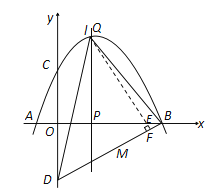

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共![]() 个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
摸球的次数 |
|
|
|
|
|
|
摸到红球的次数 |
|
|
|
|
|
|
摸到红球的频率 |
|
|
|
|
|
|
(1)试估计:盒子中有红球 个;
(2)若从盒子中一次性摸出两个球,用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率.
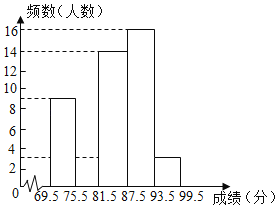
【题目】我市要开展“不忘初心,牢记使命”主题演讲比,某中学将参加本校选拔赛的50名选手的成绩(满分为100分,得分为正整数)分成五组,并绘制了不完整的统计图表.
分数段 | 频数 | 频率 |
69.5~75.5 | 9 | 0.18 |
75.5~81.5 | m | 0.16 |
81.5~87.5 | 14 | 0.28 |
87.5~93.5 | 16 | n |
93.5~99.5 | 3 | 0.06 |
(1)表中n= ,并在图中补全频数直方图.
(2)甲同学的比赛成绩是50位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(3)选拔赛时,成绩在93.5~99.5的三位选手中,男生2人,女生1人,学校从中随机确定2名选手参加全市决赛,请用列表法或树状图法求恰好是一名男生和一名女生的概率.