题目内容
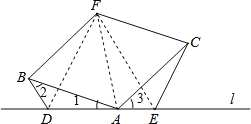
【题目】如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连结DF、EF,判断△DEF的形状,并说明理由.

【答案】(1)见解析;(2)△DEF是等边三角形,理由见解析
【解析】(1)利用菱形的性质得出AB=AC,进而得出∠2=∠3,即可利用AAS证明△ABD≌△CAE;
(2)易证△ABF与△ACF均为等边三角形,然后证明△FBD≌△FAE,则DF=EF,∠BFD=∠AFE,从而求得∠DFE的度数,即可证得:△DEF是等边三角形.
(1)证明:∵四边形ABFC为菱形,
∴AB=AC.
∵∠BDA=∠BAC=∠CEA,
又∵![]()
∴∠2=∠3.
在△ABD和△CAE中,
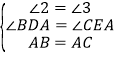
∴△ABD≌△CAE(AAS);
(2)答:△DEF是等边三角形.
连结AF,
∵四边形ABFC为菱形,![]()
∴△ABF与△ACF均为等边三角形,
∴BF=AF,![]()
∵∠2=∠3,
∴∠FBA+∠2=∠FAC+∠3,即∠FBD=∠FAE,
∵△ABD≌△CAE,
∴BD=AE.
在△FBD和△FAE中,
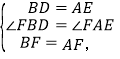
∴△FBD≌△FAE,
∴DF=EF,∠BFD=∠AFE.
∵![]()
∴![]() 即
即![]()
∴△DEF是等边三角形.

练习册系列答案
相关题目