题目内容
8．
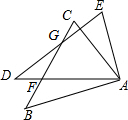如图，△ABC≌△ADE，∠C=50°，∠D=45°，∠CFA=75°，求∠BAC和∠BAE的度数．
分析 根据全等三角形的性质求出∠B和∠EAD=∠BAC，根据三角形内角和定理求出∠BAC，根据三角形的外角性质求出∠FAB，即可求出答案．
解答 解：∵△ABC≌△ADE，∠C=50°，∠D=45°，
∴∠B=∠D=45°，
∴∠BAC=180°-∠B-∠C=180°-45°-50°=85°，
∵△ABC≌△ADE，∠C=50°，∠D=45°，
∴∠EAD=∠BAC=85°，
∵∠CFA=75°，∠B=45°，
∴∠FAB=∠CFA-∠B=30°，
∴∠BAE=∠DAE+∠FAB=85°+30°=115°．
点评 本题考查了全等三角形的性质，三角形的内角和定理，三角形外角性质的应用，能正确运用知识点求出各个角的度数是解此题的关键，注意：全等三角形的对应角相等．
练习册系列答案
阅读快车系列答案
相关题目
19．
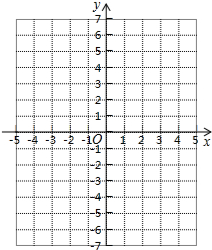已知动点（x，y）的横纵坐标满足方程2y-x=2．
（1）请在表格中求出相应的x（或y）的值，并在图中平面直角坐标系中描出这些点：
（2）若将这五个点先向右平移5个单位长度，再向上平移3个单位长度，得到点A1，B1，C1，D1，E1，并分别写出它们的坐标．
已知动点（x，y）的横纵坐标满足方程2y-x=2．（1）请在表格中求出相应的x（或y）的值，并在图中平面直角坐标系中描出这些点：
| 点的名称 | A | B | C | D | E |
| 点的横坐标x | -2 | 2 | |||
| 点的纵坐标y | -1 | 1 | 3 |
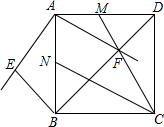如图，在正方形ABCD中，AB=2$\sqrt{2}$，将∠BAD绕着点A顺时针旋转α°（0＜α＜45），得到∠B′AD′，其中过点B作与对角线BD垂直的直线交射线AB′于点E，射线AD′与对角线BD交于点F，连接CF，并延长交AD于点M，作∠BCM的角平分线交AB于点N，当满足S四边形AEBF=$\sqrt{2}$S△CDM时，线段BN的长度为2$\sqrt{3}$-2．