题目内容
4.(1)解方程:x2-1=2(x+1)(2)计算:2cos30°-tan45°-$\sqrt{(1-tan60°)^{2}}$.
分析 (1)先移项合并同类项,再用十字相乘法分解因式对方程进行化简,最后解方程;
(2)代入特殊角的三角函数值,求解即可.
解答 解:(1)x2-1=2(x+1),
移项,得x2-1-2x-2=0,即x2-2x-3=0,
分解因式,得(x-3)(x+1)=0,
解得x1=3,x2=-1.
(2)原式=2×$\frac{\sqrt{3}}{2}$-1-$\sqrt{{(1-\sqrt{3})}^{2}}$
=$\sqrt{3}$-1-($\sqrt{3}$-1)
=0.
点评 本题考查了因式分解法解方程以及特殊角的三角函数的应用,解题的关键是会用十字相乘法分解因式以及牢记特殊角的三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )| A. | 过一点有无数条直线 | |
| B. | 两点之间线段的长度,叫做这两点之间的距离 | |
| C. | 两点确定一条直线 | |
| D. | 两点之间,线段最短 |
 如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.
如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.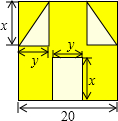 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y. +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6 如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小.
如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.