题目内容
如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.
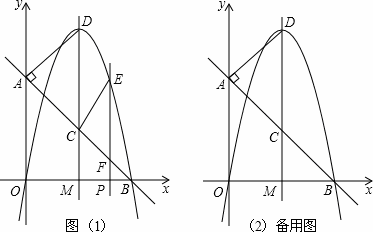

(1)直接写出直线AB的解析式;
(2)求点D的坐标;
(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=﹣x+4 (2)
(2) D(2,6)(3)点P的坐标为(
D(2,6)(3)点P的坐标为(
 ,0)或(
,0)或(
 ,0)
,0)

(2)过D点作DG⊥y轴,垂足为G,



(3)存在。
由抛物线过O(0,0),B(4,0)两点,设抛物线解析式为y=ax(x﹣4),

①当∠ECF=∠BPF=90°时(如图1),△BPF与△FCE相似,过C点作CH⊥EF,



②当∠CEF=∠BPF=90°时(如图2),


此时,△CEF、△BPF为等腰直角三角形。
则PE=MC=2,
将E(x,2)代入抛物线y=
 x(x﹣4)中,
x(x﹣4)中,
得2=
 x(x﹣4),解得x=
x(x﹣4),解得x=
 或
或
 。
。
∴P(
 ,0)。
,0)。
综上所述,点P的坐标为(
 ,0)或(
,0)或(
 ,0)。
,0)。


练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 B是⊙O的一条弦,点C是⊙O优弧AB上一动点,且∠ACB=45°,点E
B是⊙O的一条弦,点C是⊙O优弧AB上一动点,且∠ACB=45°,点E 、F分别是AC、BC的中点,直线EF与⊙O交于G、
、F分别是AC、BC的中点,直线EF与⊙O交于G、 H两点,若⊙O的半径为7,则GE+FH的最大值为 .
H两点,若⊙O的半径为7,则GE+FH的最大值为 .
 做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。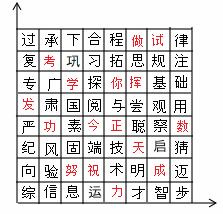
 的相邻矩形的一边均在同一直线上,点M1,M2,M3,……Mn分别为边B1B2,B2B3,B3B4,……,BnBn+1的中点,△B1C1M
的相邻矩形的一边均在同一直线上,点M1,M2,M3,……Mn分别为边B1B2,B2B3,B3B4,……,BnBn+1的中点,△B1C1M 1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn
1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn 的面积为Sn,则Sn= 。(用含n的式子表示)
的面积为Sn,则Sn= 。(用含n的式子表示)
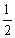 B.
B. 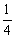 C.
C. 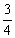 D.1
D.1 
 在第四象限,则点Q
在第四象限,则点Q 在第______象限。
在第______象限。