��Ŀ����
����������12�֣���ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��4��n���ڱ�AB�ϣ�����������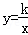 ��k��0���ڵ�һ�����ڵ�ͼ����D��E����D��ĺ������������������2����
��k��0���ڵ�һ�����ڵ�ͼ����D��E����D��ĺ������������������2����
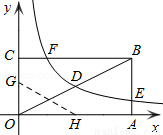
��1�����AB�ij���
��2�����������Ľ���ʽ��n��ֵ��
��3����������������ͼ������εı�BC���ڵ�F���������۵���ʹ��O���F�غϣ��ۺ۷ֱ���x��y�������ύ�ڵ�H��G�����߶�OG�ij���
��1��BA��2����2�������������Ĺ�ϵʽΪy��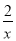 �� n��
�� n��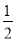 ����3��OG��
����3��OG��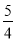 ��
��
��������
��1����E��4��n������OA��4����D�������������������2������BA��OA��1��2����BA��4��1��2����BA��2��
��2����OA��4��AB��2����B��4��2�����ߵ�DΪOB���е㣬��D��2��1�����ߵ�D�ڷ�����������ͼ���ϣ�
��1��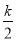 ����k��2���෴���������Ĺ�ϵʽΪy��
����k��2���෴���������Ĺ�ϵʽΪy��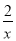 ����E��4��n���ڷ�����������ͼ���ϣ���n��
����E��4��n���ڷ�����������ͼ���ϣ���n��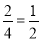 ��
��
��3����B��4��2����BC��x�ᣬ���F�����������2���ߵ�FҲ�ڷ�����������ͼ���ϣ���F��1��2������CF��1������GF����OG��GF��x����OC��2��CF2��GF2����Rt��GCF�У�CG2��CF2��GF2������2��x��2��12��x2�����x��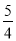 ����x��
����x��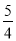 ����OG��
����OG��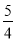 ��
��
���㣺�����������ۺ��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
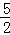 D.��2
D.��2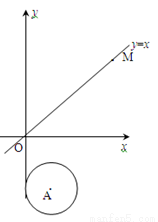
 B.
B. C.
C. D.1
D.1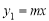 ��˫����
��˫����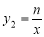 �ཻ��
�ཻ��
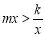 ʱ��
ʱ��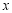 ��ȡֵ��Χ��
��ȡֵ��Χ��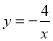 ����
����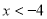 ʱ��
ʱ�� ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��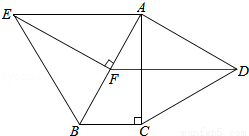
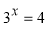 ,
, ����
����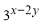 ��ֵΪ�� ��
��ֵΪ�� ��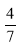 B��
B��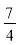 C��
C��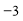 D��
D��