��Ŀ����
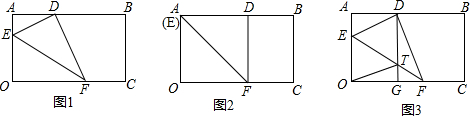
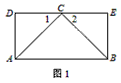
��ͼ1����֪����ABED����C�DZ�DE���е㣬��AB=2AD��

��1���жϡ�ABC����״����˵�����ɣ�
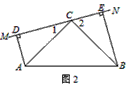
��2������ͼ1��ABC�̶����䣬�Ƶ�C��תDE���ڵ�ֱ��MN��ͼ2�У������߶�AD��BE��ֱ��MN��ͬ�ࣩ����̽���߶�AD��BE��DE����֮����ʲô��ϵ��������֤����
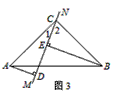
��3������ͼ2�С�ABC�̶����䣬�����Ƶ�C��תDE���ڵ�ֱ��MN��ͼ3�е�λ�ã������߶�AD��BE��ֱ��MN����ࣩ����̽���߶�AD��BE��DE����֮����ʲô��ϵ��������֤����
��2������ͼ1��ABC�̶����䣬�Ƶ�C��תDE���ڵ�ֱ��MN��ͼ2�У������߶�AD��BE��ֱ��MN��ͬ�ࣩ����̽���߶�AD��BE��DE����֮����ʲô��ϵ��������֤����
��3������ͼ2�С�ABC�̶����䣬�����Ƶ�C��תDE���ڵ�ֱ��MN��ͼ3�е�λ�ã������߶�AD��BE��ֱ��MN����ࣩ����̽���߶�AD��BE��DE����֮����ʲô��ϵ��������֤����
| �⣺��1����ABCΪ����ֱ�������Ρ� ��ͼ1���ھ���ABED�У� �ߵ�C�DZ�DE���е㣬��AB=2AD�� ��AD=DC=CE=EB��DD=DE=90�㣬 ��Rt��ADC��Rt��BEC�� ��AC=BC����1=��2=45�㣬 ���ACB=90�㣬 ���ABCΪ����ֱ�������Σ� ��2��DE=AD+BE�� ��ͼ2����Rt��ADC��Rt��CEB�У� �ߡ�1+��CAD=90�㣬��1+��2=90�㣬 ���CAD=��2�� �֡�AC=CB����ADC=��CEB=90�㣬 ��Rt��ADC��Rt��CEB�� ��DC=BE��CE=AD�� ��DC+CE=BE+AD����DE=AD+BE�� ��3��DE=BE-AD�� ��ͼ3��Rt��ADC��Rt��CEB�У� �ߡ�1+��CAD=90�㣬��1+��2=90�㣬 ���CAD=��2�� �֡ߡ�ADC=��CEB=90�㣬AC=CB�� ��Rt��ADC��Rt��CEB�� ��DC=BE��CE=AD�� ��DC-CE=BE-AD����DE=BE-AD�� |
   |

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ