题目内容
 如图,已知抛物线y=x2-1的顶点坐标为M,与x轴交于A、B两点.
如图,已知抛物线y=x2-1的顶点坐标为M,与x轴交于A、B两点.(1)判断△MAB的形状,并说明理由;
(2)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC、MD,试判断MC、MD是否垂直,并说明理由.
考点:二次函数综合题
专题:
分析:(1)由抛物线的解析式可知OA=OB=OM=1,得出∠AMO=∠MAO=∠BMO=∠MBO=45°从而得出△MAB是等腰直角三角形.
(2)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2-1),C(n,n2-1),通过EG∥DH,得出
=
,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠DMH=90°,即可求得结论.
(2)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2-1),C(n,n2-1),通过EG∥DH,得出
| EC |
| DF |
| OE |
| OF |
解答:解:(1)△MAB是等腰直角三角形. 理由如下:
理由如下:
由抛物线的解析式为:y=x2-1可知A(-1,0),B(1,0),
∴OA=OB=OM=1,
∴∠AMO=∠MAO=∠BMO=∠MBO=45°,
∴∠AMB=∠AMO+∠BMO=90°,AM=BM,
∴△MAB是等腰直角三角形.
(2)MC⊥MD.理由如下:
分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,
设D(m,m2-1),C(n,n2-1),
∴OE=-n,CE=1-n2,OF=m,DF=m2-1,
∵OM=1,
∴CG=n2,DH=m2,
∵EG∥DH,
∴
=
,
即
=
,
解得m=-
,
∵
=
=-n,
=
=
=-n,
∴
=
,
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MD.
 理由如下:
理由如下:由抛物线的解析式为:y=x2-1可知A(-1,0),B(1,0),
∴OA=OB=OM=1,
∴∠AMO=∠MAO=∠BMO=∠MBO=45°,
∴∠AMB=∠AMO+∠BMO=90°,AM=BM,
∴△MAB是等腰直角三角形.
(2)MC⊥MD.理由如下:
分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,
设D(m,m2-1),C(n,n2-1),
∴OE=-n,CE=1-n2,OF=m,DF=m2-1,
∵OM=1,
∴CG=n2,DH=m2,
∵EG∥DH,
∴
| EC |
| DF |
| OE |
| OF |
即
| 1-n2 |
| m2-1 |
| -n |
| m |
解得m=-
| 1 |
| n |
∵
| CG |
| GM |
| n2 |
| -n |
| MH |
| DH |
| m |
| m2 |
| 1 |
| m |
∴
| CG |
| GM |
| MH |
| DH |
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MD.
点评:本题考查了待定系数法求解析式,等腰三角形的判定,三角形相似的判定和性质,作出辅助线是本题的关键.

练习册系列答案
相关题目
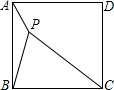 已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )
已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )| A、120? | B、125? |
| C、135? | D、150? |
某厂2013年的生产总值为a万元,2014年的生产总值比2013年增长了10%,那么该厂2014年的生产总值是( )
| A、10%a |
| B、(10%+a) |
| C、(1+10%)a |
| D、[a+(1+10%)a |
方程x2=x的解是( )
| A、x=1 | B、x=0 |
| C、x=±1 | D、x=1或0 |
代数式-2x,5,3x-y,x2y,
中,单项式的个数有( )
| x+y |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图:三角形有
如图:三角形有