题目内容
3.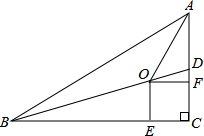 如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
分析 (1)过点O作OM⊥AB,由角平分线的性质得OE=OM,由正方形的性质得OE=OF,易得OM=OF,由角平分线的判定定理得点O在∠BAC的平分线上;
(2)由勾股定理得AB的长,利用方程思想解得结果.
解答 (1)证明:过点O作OM⊥AB,
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴$\left\{\begin{array}{l}{x+y=12}\\{y+z=13}\\{x+z=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=10}\\{z=3}\end{array}\right.$,
∴CE=2,
∴OE=2.
点评 本题主要考查了正方形的性质,以及角平分线定理及性质,熟练掌握正方形的性质,运用方程思想是解本题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
13.一条东西走向的道路上,小明先向西走5米,记作“-5米”,他又向西走了2米,此时小明的位置可记作( )
| A. | +2米 | B. | +7米 | C. | -3米 | D. | -7米 |
8.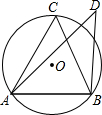 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
13.解不等式2x≥x-1,并把解集在数轴上表示( )
| A. |  | B. |  | C. |  | D. |  |
 已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.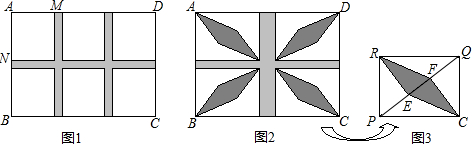
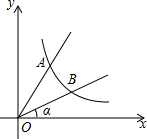 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$. 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.