题目内容
如图(1),AB∥CD,则∠A+∠C+∠E= °.在图(2)(3)中,∠A、∠E、∠C之间分别具有什么关系?


考点:平行线的性质
专题:
分析:(1)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)根据AB∥CD,可得∠A=∠1,再根据三角形内角与外角的性质可得∠C+∠E=∠1,根据等量代换可得∠A=∠C+∠E.
(2)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)根据AB∥CD,可得∠A=∠1,再根据三角形内角与外角的性质可得∠C+∠E=∠1,根据等量代换可得∠A=∠C+∠E.
解答:解:图(1)∠A+∠E+∠C=360°,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠BAE+∠1=180°,∠2+∠ECD=180°,
∴∠BAE+∠1+∠2+∠ECD=360°,
∴∠AEC+∠EAB+∠ECD=360°,
故答案为:360;

图(2)∠AEC=∠BAE+∠ECD,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠BAE,∠2=∠ECD,
∴∠AEC=∠1+∠2=∠BAE+∠ECD;
图(3),∠A=∠C+∠E,
∵AB∥CD,
∴∠A=∠1,
∵∠C+∠E=∠1,
∴∠A=∠C+∠E.
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠BAE+∠1=180°,∠2+∠ECD=180°,
∴∠BAE+∠1+∠2+∠ECD=360°,
∴∠AEC+∠EAB+∠ECD=360°,
故答案为:360;

图(2)∠AEC=∠BAE+∠ECD,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠BAE,∠2=∠ECD,
∴∠AEC=∠1+∠2=∠BAE+∠ECD;
图(3),∠A=∠C+∠E,
∵AB∥CD,
∴∠A=∠1,
∵∠C+∠E=∠1,
∴∠A=∠C+∠E.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
下列分式中是最简分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如果有理数x、y满足|x-1|+(y+3)2=0,则(xy)2的值是( )
| A、6 | B、-6 | C、9 | D、-9 |
 将一副三角板如图叠放,AB∥CD,则
将一副三角板如图叠放,AB∥CD,则| AO |
| OC |
| A、1:2 | ||
| B、2:3 | ||
C、1:
| ||
D、
|
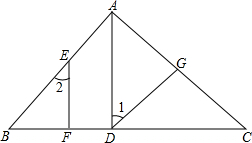 如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由.
如图,在△ABC中,AD⊥BC于点D,EF⊥BC于点F,∠B=∠GDC,试说明∠1=∠2的理由. 如图,已知
如图,已知