题目内容
18. 如图,在下列解答中,填写适当的理由或数学式:
如图,在下列解答中,填写适当的理由或数学式:(1)∵AB∥DC(已知)
∴∠B=∠DCE;(两直线平行,同位角相等)
(2)∵AB∥DC(已知)
∴∠ACD=∠BAC(两直线平行,内错角相等)
(3)∵∠B+∠BAD=180°(已知)
∴AD∥BE(同旁内角互补,两直线平行)
(4)∵∠DAC=∠ACB(已知)
∴AD∥BE(内错角相等,两直线平行)
分析 (1)根据两直线平行,同位角相等得出即可;
(2)根据两直线平行,内错角相等得出即可;
(3)根据同旁内角互补,两直线平行得出即可;
(4)根据内错角相等,两直线平行得出即可.
解答 解:(1)∵AB∥DC,(已知),
∴∠B=∠DCE;(两直线平行,同位角相等),
故答案为:DCE,两直线平行,同位角相等;
(2)∵AB∥DC,(已知)
∴∠ACD=∠BAC;(两直线平行,内错角相等 )
故答案为:AB,DC,两直线平行,内错角相等;
(3)∵∠B+∠BAD=180°,(已知)
∴AD∥BE;(同旁内角互补,两直线平行 ),
故答案为:AD,BE,同旁内角互补,两直线平行;
(4)∵∠DAC=∠ACB,(已知)
∴AD∥BE.(内错角相等,两直线平行),
故答案为:AD,BE,内错角相等,两直线平行.
点评 本题考查了平行线的性质和判定定理的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
10. 如图,用12米长的木条做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的高AB(木条粗细忽略不计)为( )
如图,用12米长的木条做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的高AB(木条粗细忽略不计)为( )
 如图,用12米长的木条做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的高AB(木条粗细忽略不计)为( )
如图,用12米长的木条做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的高AB(木条粗细忽略不计)为( )| A. | 1米 | B. | 2米 | C. | 3米 | D. | 4米 |
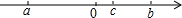 a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.
a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值. 如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想.
如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想.