��Ŀ����
��10�֣�Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в��ü۸���ص��ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѵļ�Ŀ�����±���ע��ˮ�Ѱ��·ݽ��㣬m3��ʾ�����ף���
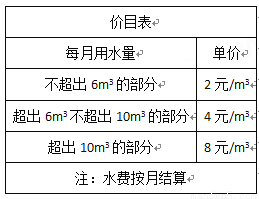
������ϱ������ݽ���������⣺
��1����գ����û�����2�·���ˮ4m3����Ӧ��ˮ��_____Ԫ��
��2�����û�����3�·���ˮam3������6m3��a��10m3������Ӧ��ˮ�Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������
��3�����û�����4��5�����¹���ˮ15m3������4�·���ˮ��������6 m3����4�·���ˮxm3����û�����4��5�����¹���ˮ�Ѷ���Ԫ�����ú�x�Ĵ���ʽ��ʾ��������
 ��1��8Ԫ ����2��4a-12����3��48-2x��68-6x
��������������������ڣ�1����������6m3������Ϊ2Ԫ��ˮ��=���ۡ��������ݴ˽��
���ڣ�2�����������ˮ��=����Ϊ2Ԫ��6m3��ˮ��+����Ϊ4Ԫ�ij���6m3��ˮ�ѣ�
���ڣ�3��Ӧ��������ۣ�4�·ݲ�����6m3��5�·�10���������ϣ���4�·ݲ�����6m3��5�·���6-10������֮��.
��������
��1��2��4=...
��1��8Ԫ ����2��4a-12����3��48-2x��68-6x
��������������������ڣ�1����������6m3������Ϊ2Ԫ��ˮ��=���ۡ��������ݴ˽��
���ڣ�2�����������ˮ��=����Ϊ2Ԫ��6m3��ˮ��+����Ϊ4Ԫ�ij���6m3��ˮ�ѣ�
���ڣ�3��Ӧ��������ۣ�4�·ݲ�����6m3��5�·�10���������ϣ���4�·ݲ�����6m3��5�·���6-10������֮��.
��������
��1��2��4=...
��ͼ,��һ�ų�����ֽƬABCD��ͼ�еķ�ʽ�۵�,ʹ��A���E�غ�,��C���F�غ�(E,F�������BD��),�ۺ۷ֱ�ΪBH,DG.��˵��:��BHE�ա�DGF.
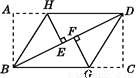
 ������
������������������ȸ��ݾ��ε����ʵó���ABD=��BDC������ͼ���۵������ʵó���ABH=��EBH����FDG=��CDG����A=��HEB=90�㣬��C=��DFG=90�㣬�����ɵó���BEH�ա�DFG.
������������ı���ABCD�dz����Σ�
��AB=CD����A=��C=90�㣬��ABD=��BDC��
�ߡ�BEH�ǡ�BAH���۶��ɣ�
���ABH=��EBH����A=��HEB...
������
������������������ȸ��ݾ��ε����ʵó���ABD=��BDC������ͼ���۵������ʵó���ABH=��EBH����FDG=��CDG����A=��HEB=90�㣬��C=��DFG=90�㣬�����ɵó���BEH�ա�DFG.
������������ı���ABCD�dz����Σ�
��AB=CD����A=��C=90�㣬��ABD=��BDC��
�ߡ�BEH�ǡ�BAH���۶��ɣ�
���ABH=��EBH����A=��HEB... ��ͼ,�������߳���ԳƵ���(����)��.

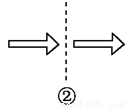
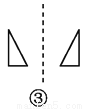
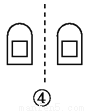
A. 1 B. 2 C. 3 D. 4
 B
���������ٹ������߲�����Գƣ��ڹ������߲�����Գƣ��۹������߲�����Գƣ��ܹ������߳���Գƣ�
��ѡB.
B
���������ٹ������߲�����Գƣ��ڹ������߲�����Գƣ��۹������߲�����Գƣ��ܹ������߳���Գƣ�
��ѡB. ���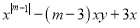 Ϊ�Ĵ�����ʽ����
Ϊ�Ĵ�����ʽ����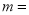 ___________��
___________��
 -1
���������������
��m-3��0,
��֮��
m=-1.
-1
���������������
��m-3��0,
��֮��
m=-1. ���㣺��ÿС��5��,��10�֣�
��1��5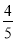 ��2
��2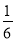 ������4.8��+����4
������4.8��+����4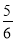 �� ��2����
�� ��2����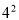 ��3��
��3��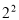 ����
����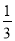 �������£�����
�������£�����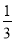 ��
��
 ��1��-6����2��-22
�������������������1�����üӷ��Ľ����ɺͽ���ɼ��㣬��һ�������ϣ����������ϣ���2����������˷�������˳�������Ӽ��������ŵ������������˳�����.
��������
��1��5��2������4.8��+����4��
=5������4��+����4��+����2��
=1-7
=-6��
��2������3�������������£�������
=-16-3��4��(-) ��(-)...
��1��-6����2��-22
�������������������1�����üӷ��Ľ����ɺͽ���ɼ��㣬��һ�������ϣ����������ϣ���2����������˷�������˳�������Ӽ��������ŵ������������˳�����.
��������
��1��5��2������4.8��+����4��
=5������4��+����4��+����2��
=1-7
=-6��
��2������3�������������£�������
=-16-3��4��(-) ��(-)... ��ͼ,��ֱ֪��a,b,c,d,e,�ҡ�1=��2,��3+��4=180��,��a��cƽ����?Ϊʲô?
��:a��cƽ��.
����:����1=��2(����),
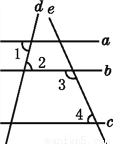
����a��b (������������ ��������).
����3+��4=180��(��������),
����b��c (������������������).
����a��c (������������������������������).
 ��֪;�ڴ������,��ֱ��ƽ��;��֪;ͬ���ڽǻ���,��ֱ��ƽ��;�������ֱ�߶��������ֱ��ƽ��,��ô������ֱ��Ҳ����ƽ��
���������������������ƽ���ߵ����ʵó�a��b��b��c�������Ƴ��𰸣�
���������a��c��
�����ǣ��ߡ�1=��2(��֪)��
��a��b(�ڴ�����ȣ���ֱ��ƽ��)��
�ߡ�3+��4=180��(��֪)��
��b��c(ͬ���ڽǻ�������ֱ��ƽ��)��
��a...
��֪;�ڴ������,��ֱ��ƽ��;��֪;ͬ���ڽǻ���,��ֱ��ƽ��;�������ֱ�߶��������ֱ��ƽ��,��ô������ֱ��Ҳ����ƽ��
���������������������ƽ���ߵ����ʵó�a��b��b��c�������Ƴ��𰸣�
���������a��c��
�����ǣ��ߡ�1=��2(��֪)��
��a��b(�ڴ�����ȣ���ֱ��ƽ��)��
�ߡ�3+��4=180��(��֪)��
��b��c(ͬ���ڽǻ�������ֱ��ƽ��)��
��a... ��ͼ,�ڡ�ABC��,��BAC=4��ABC=4��C,BD��AC��CA���ӳ����ڵ�D,���ABD�Ķ���.
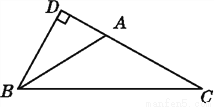
 30��.
��������������������������ε��ڽǺ�Ϊ180�㼴�ɵõ���ABC���C�Ķ���������������ǿ���á�DAB�Ķ������Ӷ���á�ABD�Ķ�����
����������ߡ�BAC=4��ABC=4��C��
���BAC+��ABC+��C=180�㣬
����C=��ABC=180��=30�㣬
���DAB=��C+��ABC=30��+30��=60�㣬
��BD��AC��
���BDA=90�㣬...
30��.
��������������������������ε��ڽǺ�Ϊ180�㼴�ɵõ���ABC���C�Ķ���������������ǿ���á�DAB�Ķ������Ӷ���á�ABD�Ķ�����
����������ߡ�BAC=4��ABC=4��C��
���BAC+��ABC+��C=180�㣬
����C=��ABC=180��=30�㣬
���DAB=��C+��ABC=30��+30��=60�㣬
��BD��AC��
���BDA=90�㣬... 

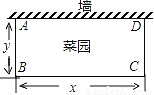
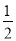 x+12 B. y=��2x+24 C. y=2x��24 D. y=
x+12 B. y=��2x+24 C. y=2x��24 D. y=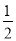 x��12
x��12