题目内容
 如图,在△ABC中,AB=AC,D为△ABC内一点,且∠1=∠2,若∠A=50°,则∠BDC=
如图,在△ABC中,AB=AC,D为△ABC内一点,且∠1=∠2,若∠A=50°,则∠BDC=考点:等腰三角形的性质
专题:
分析:根据等边对等角可得∠ABC=∠ACB,然后求出∠1+∠BCD=∠ACB,再根据三角形的内角和定理列式计算即可得解.
解答:解:∵AB=AC,∠A=50°,
∴∠ABC=∠ACB=
(180°-50°)=65°,
∵∠1=∠2,
∴∠1+∠BCD=∠ACB=65°,
在△BCD中,∠BDC=180°-(∠1+∠BCD)=180°-65°=115°.
故答案为:115.
∴∠ABC=∠ACB=
| 1 |
| 2 |
∵∠1=∠2,
∴∠1+∠BCD=∠ACB=65°,
在△BCD中,∠BDC=180°-(∠1+∠BCD)=180°-65°=115°.
故答案为:115.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,熟记性质并求出∠1+∠BCD的度数是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
方程x2-3x-2=0的根的情况是( )
| A、方程有两个相等的实数根 |
| B、方程有两个不相等的实数根 |
| C、方程没有实数根 |
| D、方程的根的情况无法确定 |
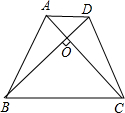 如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高.
如图,已知在等腰梯形ABCD中,AD∥BC,AC⊥BD,且梯形ABCD的面积为100cm2,求梯形的高.