题目内容
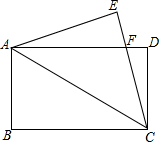 如图,在长方形ABCD中,AB=4,BC=8,将△ABC沿着AC对折至△AEC位置,CE与AD交于点F,则AF的长为( )
如图,在长方形ABCD中,AB=4,BC=8,将△ABC沿着AC对折至△AEC位置,CE与AD交于点F,则AF的长为( )| A、3 | B、4 | C、5 | D、6 |
考点:翻折变换(折叠问题)
专题:
分析:证明FA=FC,此为解决该题的关键性结论;运用勾股定理列出关于线段CF的方程,即可解决问题.
解答: 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,
∴AD=BC=8,DC=AB=4;
AD∥BC,∠D=90°;
∴∠FAC=∠ACB;
由题意得:∠FCA=∠ACB,
∴∠FAC=∠FCA,
∴FA=FC(设为λ),则DF=8-λ;
由勾股定理得:λ2=(8-λ)2+42,
解得:λ=5,
故选C.
 解:∵四边形ABCD为矩形,
解:∵四边形ABCD为矩形,∴AD=BC=8,DC=AB=4;
AD∥BC,∠D=90°;
∴∠FAC=∠ACB;
由题意得:∠FCA=∠ACB,
∴∠FAC=∠FCA,
∴FA=FC(设为λ),则DF=8-λ;
由勾股定理得:λ2=(8-λ)2+42,
解得:λ=5,
故选C.
点评:该题以矩形为载体,以翻折变换为方法,以考查矩形的性质、勾股定理等几何知识点为核心构造而成;灵活运用等腰三角形的判定、勾股定理等知识点来分析、判断、推理或解答是关键.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1cm,则线段AB=( )cm.
如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1cm,则线段AB=( )cm.| A、1 | B、2 | C、4 | D、8 |
 如图,数轴上点A,B对应的数分别为1,
如图,数轴上点A,B对应的数分别为1,| 7 |
A、
| ||
B、
| ||
C、1-
| ||
D、2-
|
如果(an•bm•b)3=a9b15,那么m,n的值等于( )
| A、m=9,n=-4 |
| B、m=3,n=4 |
| C、m=4,n=3 |
| D、m=9,n=6 |
 某同学为了解所住小区家庭月均用水情况,调查了该小区所有200户家庭,并将调查数据整理如表:
某同学为了解所住小区家庭月均用水情况,调查了该小区所有200户家庭,并将调查数据整理如表: