题目内容
19.在△ABC中,∠C=90°,∠A=15°,AB=12,求△ABC的面积.分析 根据题意画出图形,进而在AC上取一点D,使AD=BD,则利用直角三角形的性质求出答案.
解答  解:在AC上取一点D,使AD=BD,
解:在AC上取一点D,使AD=BD,
∵∠C=90°,∠A=15°,AD=BD,
∴∠A=∠ABD=15°,
∴∠BDC=30°,
设BC=x,则BD=2x,
故CD=$\sqrt{3}$x,
在Rt△ABC中,
BC2+AC2=AB2,
则x2+(2x+$\sqrt{3}$x)2=122,
解得:x2=36(2-$\sqrt{3}$),
S△ABC=$\frac{1}{2}$BC×AC=$\frac{1}{2}$x(2x+$\sqrt{3}$x)=$\frac{1}{2}$x2(2+$\sqrt{3}$)=18.
点评 此题主要考查了勾股定理以及直角三角形的性质,得出x2的值是解题关键.

练习册系列答案
相关题目
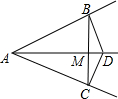 点D是∠BAC的平分线上一点,过点D作DB⊥AB于点B,DC⊥AC于点C,连接BC交AD于点M.求证:
点D是∠BAC的平分线上一点,过点D作DB⊥AB于点B,DC⊥AC于点C,连接BC交AD于点M.求证: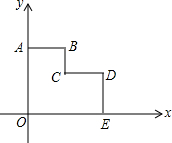 如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.
如图,在平面直角坐标系xOy中,多边形OABCDE的顶点分别为O(0,0)、A(0,8)、B(4,8)、C(4,4)、D(8,4)、E(8,0),若直线l经过点M(3,$\frac{7}{2}$),分别与边OA、DE相交且将多边形OABCDE面积平分.