题目内容
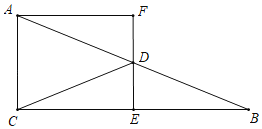
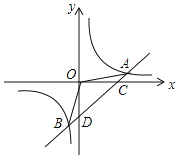
【题目】花园小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高4米的小区商场，商场以上是居民住房．在该楼的前面16米处要盖一栋高18米的办公楼．当冬季正午的阳光与水平线的夹角为
时，问：
（1）商场以上的居民住房采光是否有影响，为什么？
（2）若要使商场采光不受影响，两楼应相距多少 米？（结果保留一位小数）
（参考数据：
，
，
）
【答案】(1) 居民住房的采光有影响,理由见解析；（2）两楼相距25.8米
【解析】
（1）求是否影响采光，就是求办公楼在居民楼上的影子部分是否高过4米，设光线交居民楼于E，那么就是求DE的长度，过点
作
交
于点
，设
米，则
米，在
中，
，根据
列出方程即可。
（2）要想商场采光不受影响，那么办公楼的影子的长度等于BD，在直角三角形ABD中，AB=18，∠ADB=
那么根据
求得BD的值即可．
解：（1）如图，光线交
于点，过点作交于点．
则四边形BDEF为矩形，∴EF=BD，BF=DE；
设米，则米.
在中，
，
，
，
居民住房的采光有影响．
（2）如图，在
中，
，
（米）.
答：两楼相距25.8米．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
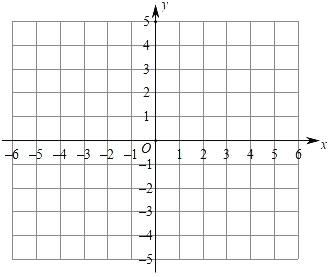
【题目】小明对函数y＝﹣|x2﹣4|的图象和性质进行了探究，其探究过程中的列表如下：
x | … | -3 | ﹣2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 0 | -3 | n | -3 | 0 | -5 | … |
（1）求表中m，n的值；
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了该函数的图象；
（3）观察函数图象，写出一条函数的性质；
（4）结合你所画的函数图象，直接写出不等式﹣|x2﹣4|＞x﹣2的解集．
