Question

【题目】在平面直角坐标系中，抛物线与轴分别交于点、点（点在点的右侧），与轴交于点，.

（1）求抛物线的解析式；

（2）设该抛物线的顶点为，求四边形的面积；

（3）设抛物线上的点在第一象限，是以为一条直角边的直角三角形，请直接写出点的坐标.

Answer 1

【答案】（1）；（2）8；（3）或.

【解析】

（1）由抛物线解析式和已知条件得出C和B的坐标，（0，3），OC＝3，

把A（2，0）、B（6，0）分别代入y＝ax2＋bx＋3得出方程组，解方程即可；

（2）把抛物线解析式化成顶点式得出顶点坐标，四边形ACBD的面积＝△ABC的面积＋△ABD的面积，即可得出结果；

（3）设点E的坐标为（x，），分两种情况：①当∠CBE＝90°时；②当∠BCE＝90°时；分别由三角函数得出方程，解方程即可．

（1）当时，，

.

在中，

，

.

.

点.

把、分别代入，得

得

解得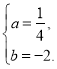

该抛物线解析式为.

（2），

顶点.

.

（3）（3）设点E的坐标为（x，），分两种情况：

①当∠CBE＝90°时，

作EM⊥x轴于M，如图所示：

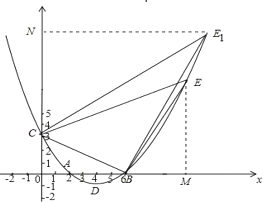
则∠BEM＝∠CBA，

∴＝tan∠BEM＝tan∠CBA＝，

∴EM＝2BM，

即2（x6）＝

解得：x＝10，或x＝6（不合题意，舍去），

∴点E坐标为（10，8）；

②当∠BCE1＝90°时，作E1N⊥y轴于N，

则∠E1CN＝∠CBA，

∴＝tan∠E1CN＝tan∠CBA＝，

∴CN＝2E1N，

即2x＝-3

解得：x＝16，或x＝0（不合题意，舍去），

∴点E1坐标为（16，35）；

综上所述：点的坐标是或.