题目内容

如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

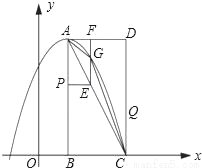
（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？

（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

（1）A（1，4）；y=﹣x2+2x+3；（2）当t=2时，S△ACG的最大值为1；（3）t=20﹣8 或t= ． 【解析】试题分析：（1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x-1）2+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；（2）利用待定系数法求得直线AC的方程y=-2x+6；由图形与坐标变换可以求得...
练习册系列答案
相关题目

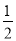如图，抛物线y=x2﹣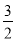x﹣9与x轴交于A、B两点，与y轴交于点C，连接BC、AC．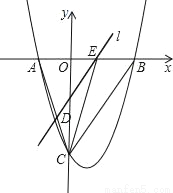

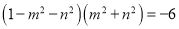（1）求AB和OC的长；

（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；

（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．

（1）AB=9，OC=9；（2）s=m2（0＜m＜9）；（3）. 【解析】试题分析：（1）已知抛物线的解析式，当 可确定点坐标；当时，可确定点的坐标，进而确定的长． （2）直线 可得出相似，它们的面积比等于相似比的平方，由此得到关于的函数关系式；根据题干条件：点与点不重合，可确定的取值范围． （3）①首先用列出的面积表达式， 的面积差即为的面积，由此可得关于的函数关系式，根据函数的性质可...

已知，则m2+n2的值是（　　）

A. 3 B. 3或-2 C. 2或-3 D. 2

A 【解析】， ， ， ， ∴或（舍去）， 故选A．

我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知：在Rt△ABC中，∠C=90°，AC=6，BC=3.

（1）如图l，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a1是________；

（2）如图2，四边形DGHI是（1）中△EDA的内接正方形，那么第2个正方形DGHI的边长记为a2；继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推，则第n个内接正方形的边长an=____. （n为正整数）

2 【解析】（1）由正方形的性质可以得出△BFE∽△BCA，再根据相似三角形的性质就可以把正方形CDEF的边长表示出来，从而得出结论． （2）由正方形的性质可以得出△EIH∽△EDA，再根据相似三角形的性质就可以把正方形IDGF的边长表示出来，从而得出结论，通过计算得出的结论寻找其中的变化规律就可以得出第n个内接正方形的边长的值． 【解析】 （1）四边形CDEF是正方形， ...

如图，D，E为△ABC的边AB，AC上的点，DE∥BC，若AD：DB=1：3，AE=2，则AC的长是（ ）.

A. 10 B. 8 C. 6 D. 4

B 【解析】∵DE//BC， ∴AE：EC=AD：DB， ∵AD：DB=1：3， ∴AE：EC=1：3， ∵AE=2，∴EC=6， ∴AC=AE+EC=8， 故选B.

某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的，而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息，解答下列问题：

(1)此次调查的学生人数为___；

(2)条形统计图中存在错误的是___(填A. B. C中的一个)，并在图中加以改正；

(3)在图2中补画条形统计图中不完整的部分；

(4)如果该校有600名学生，那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?

（1）200；（2）C （3）D的人数为30人；（4）360人. 【解析】试题分析：（1）根据A、B的人数和所占的百分比求出抽取的学生人数，并判断出条形统计图A、B长方形是正确的； （2）根据（1）的计算判断出C的条形高度错误，用调查的学生人数乘以C所占的百分比计算即可得解； （3）求出D的人数，然后补全统计图即可； （4）用总人数乘以A、B所占的百分比计算即可得解． ...

如图，在⊙O中，弦AB，CD相交于点P．若∠A=40°，∠APD=75°，则∠B=　 　．

35°． 【解析】试题解析： 故答案为：

已知质量一定的某物体的体积V（m3）是密度ρ（kg/m3）的反比例函数，其图象如图所示：

（1）请写出该物体的体积V与密度ρ的函数关系式；

（2）当该物体的密度ρ=3.2Kg/m3时，它的体积v是多少？

（3）如果将该物体的体积控制在10m3～40m3之间，那么该物体的密度应在什么范围内变化？

（1）V=；（2）10（m）3；（3）该物体的密度在0.8Kg/m3～3.2Kg/m3的范围内变化． 【解析】【试题分析】 （1）用待定系数法求解析式，设V=，根据题意，当ρ=1.6时，v=20， 即k=ρV=20×1.6=32．得V=． （2）直接代入解析式，即可.当=3.2时，V==10（m）3． （3）当V=40时， =40，∴ρ=0.8（Kg/m3）．由（2）...

等腰三角形的一个角是80°，则它的底角是（ ）

A. 50° B. 80° C. 50°或80° D. 20°或80°

C 【解析】当80°为顶角时，此时底角度数为=50°； 当80°为底角时，此时顶角度数为180-2×80°=20°. 故它的底角是50°或80°. 故选C.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网