Question

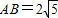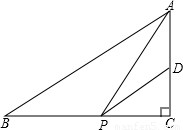
如图，直角△ABC中，∠C=90°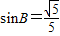，，，点P为边BC上一动点，PD∥AB，PD交AC于点D，连接AP．
（1）求AC、BC的长；
（2）设PC的长为x，△ADP的面积为y．当x为何值时，y最大，并求出最大值．

Answer 1

【答案】分析：（1）在Rt△ABC中，根据∠B的正弦值及斜边AB的长，可求出AC的长，进而可由勾股定理求得BC的长；
（2）由于PD∥AB，易证得△CPD∽△CBA，根据相似三角形得出的成比例线段，可求出CD的表达式，也就求出AD的表达式，进而可以AD为底、PC为高得出△ADP的面积，即可求出关于y、x的函数关系式，根据所得函数的性质，可求出y的最大值及对应的x的值．
解答：解：（1）在Rt△ABC中，，，
得，
∴AC=2，根据勾股定理得：BC=4；（3分）

（2）∵PD∥AB，∴△ABC∽△DPC，∴；
设PC=x，则，，
∴
∴当x=2时，y的最大值是1． （8分）
点评：此题主要考查了解直角三角形、相似三角形的判定和性质、二次函数的应用等知识．