题目内容
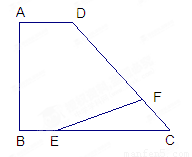
 已知,如图在直角△ABC中,∠C=90°,AE•AC=AD•AB.
已知,如图在直角△ABC中,∠C=90°,AE•AC=AD•AB.求证:ED⊥AB.
分析:把已知条件进行转换即可推出△CBA和△DEA的对应边的相似比相等,结合公共角,推出△CBA∽△DEA即可.
解答:证明:∵AE•AC=AD•AB
∴
=
∵∠A=∠A
∴△CBA∽△DEA
∵∠C=90°
∴∠EAD=90°
∴ED⊥AB.
∴
| AE |
| AB |
| AD |
| AC |
∵∠A=∠A
∴△CBA∽△DEA
∵∠C=90°
∴∠EAD=90°
∴ED⊥AB.
点评:本题主要考查相似三角形的判定和性质、垂直定义,关键是转换相关的已知条件求出相关的三角形相似.

练习册系列答案
相关题目
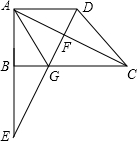

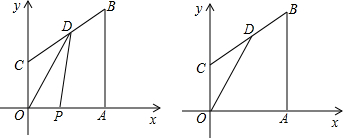
 ?
?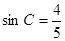 ,
,