题目内容
某人沿坡度为1:8的山坡向上走了65m,则此人上升的高度为
- A.
 m
m - B.
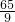 m
m - C.
 m
m - D.
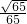 m
m
A
分析:坡度比=垂直高度:水平距离=1:8,又坡面距离已知,那么在垂直高度、水平距离、坡面距离构成直角三角形的情况下,可用勾股定理进行解答.
解答:设此人上升的高度为xm,则水平前进了8xm.
根据勾股定理可得x2+(8x)2=652解得:x= m.
m.
故选A.
点评:此题考查坡度的定义和勾股定理的应用.
分析:坡度比=垂直高度:水平距离=1:8,又坡面距离已知,那么在垂直高度、水平距离、坡面距离构成直角三角形的情况下,可用勾股定理进行解答.
解答:设此人上升的高度为xm,则水平前进了8xm.
根据勾股定理可得x2+(8x)2=652解得:x=
 m.
m.故选A.
点评:此题考查坡度的定义和勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某人沿坡度为1:8的山坡向上走了65m,则此人上升的高度为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某人沿坡度为1:
的坡面向上走50米,则他离地面的高度是( )
| 3 |
A、25
| ||
| B、50米 | ||
| C、25米 | ||
D、50
|