题目内容
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.
首先,确定自变量![]() 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被![]() 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着![]() 值的减小,
值的减小,![]() 的值会越来越大…,由此,可以大致画出
的值会越来越大…,由此,可以大致画出![]() 在
在![]() 时的部分图象,如图所示:
时的部分图象,如图所示:
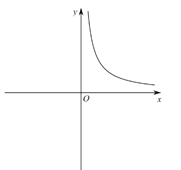
利用同样的方法,我们可以研究函数![]() 的图象与性质.通过分析解析式画出部分函数图象如图所示.
的图象与性质.通过分析解析式画出部分函数图象如图所示.
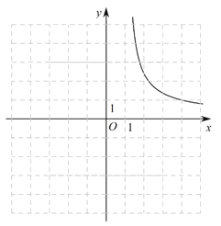
(1)请沿此思路在图中完善函数图象的草图并标出此函数图象上横坐标为0的点![]() ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)
(2)观察图象,写出该函数的一条性质:__________;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数![]() 的取值范围: __________.
的取值范围: __________.
【答案】(1)见解析;(2)当![]() 时,
时,![]() 随
随![]() 增大而减小;(3)
增大而减小;(3)![]()
【解析】
(1)先得出函数![]() 自变量
自变量![]() 的取值范围,再分析解析式,得到
的取值范围,再分析解析式,得到![]() 随
随![]() 的变化趋势,由此完善函数图象即可;令
的变化趋势,由此完善函数图象即可;令![]() 求出y的值即可得出点A坐标;
求出y的值即可得出点A坐标;
(2)根据函数图象得出其增减性即可;
(3)将所求问题看成函数![]() 与一次函数
与一次函数![]() 的交点问题,先找出一个临界位置,再根据一次函数的性质即可得.
的交点问题,先找出一个临界位置,再根据一次函数的性质即可得.
(1)由二次根式的被开方数的非负性、分式的分母不能为0得: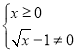
解得:![]() 且
且![]()
令![]() 得
得![]()
则点A坐标为![]()
分析解析式,得到![]() 随
随![]() 的变化趋势:当
的变化趋势:当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值会越来越小;当
的值会越来越小;当![]() 时,随着
时,随着![]() 值的增大,
值的增大,![]() 的值会减小,且逐渐接近于零,由此,完善函数图象如图所示:
的值会减小,且逐渐接近于零,由此,完善函数图象如图所示:
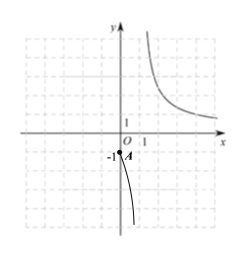
(2)由(1)图象可知,当![]() 时,
时,![]() 随
随![]() 增大而减小;(注:答案不唯一)
增大而减小;(注:答案不唯一)
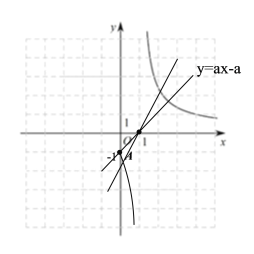
(3)由题意得,函数![]() 与一次函数
与一次函数![]() 有两个交点
有两个交点
一次函数![]() 的图象经过定点
的图象经过定点![]()
要使两个函数有两个交点,一次函数![]() 经过点
经过点![]() 是一个临界位置,此时有
是一个临界位置,此时有![]() ,即
,即![]()
因此,结合函数图象可知,当![]() 时,两个函数必有两个交点,即关于
时,两个函数必有两个交点,即关于![]() 的方程
的方程![]() 有两个不相等的实数根
有两个不相等的实数根
故答案为:![]() .
.

练习册系列答案
相关题目