题目内容
 边长为1的正方形绕着它的一个顶点旋转45°,旋转得到的正方形与原正方形重叠部分的面积等于
边长为1的正方形绕着它的一个顶点旋转45°,旋转得到的正方形与原正方形重叠部分的面积等于
- A.

- B.2-

- C.

- D.

C
分析:作CE⊥AD,CF⊥AB.则直角三角形BCF是等腰直角三角形.根据重叠部分的面积=梯形ABCF的面积-S△CEF即可求解.
解答: 解:作CE⊥AD,CF⊥AB.
解:作CE⊥AD,CF⊥AB.
∴直角三角形BCF是等腰直角三角形.
∴∠FBC=45°,
cos45°= ,
,
∴BF=BC• =
= ,
,
∴CE=1-BF=1- =
=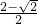 .
.
△CED是等腰直角三角形,则S△CEF= CE•DE=
CE•DE= ×
×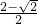 ×
×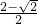 =
= .
.
梯形ABCF的面积是: (CE+AB)•CF=
(CE+AB)•CF= (
(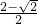 +1)•
+1)• =
= .
.
∴重叠部分的面积=梯形ABCF的面积-S△CEF= -
- =
= -1.
-1.
故选C.
点评:本题主要考查了正方形的性质,以及旋转的性质,正确作出辅助线,理解重叠部分的面积=梯形ABCF的面积-S△CEF是解题关键.
分析:作CE⊥AD,CF⊥AB.则直角三角形BCF是等腰直角三角形.根据重叠部分的面积=梯形ABCF的面积-S△CEF即可求解.
解答:
 解:作CE⊥AD,CF⊥AB.
解:作CE⊥AD,CF⊥AB.∴直角三角形BCF是等腰直角三角形.
∴∠FBC=45°,
cos45°=
 ,
,∴BF=BC•
 =
= ,
,∴CE=1-BF=1-
 =
=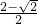 .
.△CED是等腰直角三角形,则S△CEF=
 CE•DE=
CE•DE= ×
×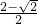 ×
×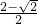 =
= .
.梯形ABCF的面积是:
 (CE+AB)•CF=
(CE+AB)•CF= (
(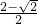 +1)•
+1)• =
= .
.∴重叠部分的面积=梯形ABCF的面积-S△CEF=
 -
- =
= -1.
-1.故选C.
点评:本题主要考查了正方形的性质,以及旋转的性质,正确作出辅助线,理解重叠部分的面积=梯形ABCF的面积-S△CEF是解题关键.

练习册系列答案
相关题目
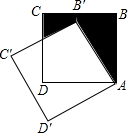 如图,边长为1的正方形ABCD绕着点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕着点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、1-
| ||||
D、1-
|

 (2008•上城区模拟)边长为1的正方形绕着它的一个顶点旋转45°,旋转得到的正方形与原正方形重叠部分的面积等于( )
(2008•上城区模拟)边长为1的正方形绕着它的一个顶点旋转45°,旋转得到的正方形与原正方形重叠部分的面积等于( )



