题目内容
设实数a、b满足不等式||a|-（a+b）|＜|a-|a+b||，则（ ）
分析：可采用排除法，取a=-1、b=2，可首先否定A、C、D选项．
解答：解：取a=-1、b=2可否定A、C、D．
一般地，对已知不等式平方，有|a|（a+b）＞a|a+b|．
显然|a||（a+b）|＞0（若等于0，则与上式矛盾），有
＞
两边都只能取1或-1，
故只有1＞-1，即
=1，
=-1，有a＜0且a+b＞0，从而b＞-a＞0．
故选B．
一般地，对已知不等式平方，有|a|（a+b）＞a|a+b|．
显然|a||（a+b）|＞0（若等于0，则与上式矛盾），有
| a+b |
| |a+b| |
| a |
| |a| |
故只有1＞-1，即
| a+b |
| |a+b| |
| a |
| |a| |
故选B．
点评：本题考查含绝对值的一元一次不等式的知识，难度较大，解题关键是对已知不等式平方，得到|a|（a+b）＞a|a+b|作为突破口．
练习册系列答案
相关题目
设x、y、z是两两不等的实数，且满足下列等式：
+
=
-
，则代数式x3+y3+z3-3xyz的值是（ ）
| 6 | x3(y-x)3 |
| 6 | x3(z-x)3 |
| 6 | y-x |
| 6 | x-z |
| A、0 | B、1 |
| C、3 | D、条件不足，无法计算 |
的值．
≠0，求m2＋
的值．
是任意两个不等实数，我们规定：满足不等式
的实数
的所有取值的全体叫做闭区间，表示为
．对于一个函数，如果它的自变量
满足：当
时，有
，我们就
称此函数是闭区间
上的“闭函数”．
是闭区间
上的“闭函数”吗？请判断并说明理由；
是闭区间
上的“闭函数”，求此函数的解析式；
是闭区间
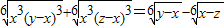，则代数式x3+y3+z3-3xyz的值是（ ）
，则代数式x3+y3+z3-3xyz的值是（ ）