题目内容
设x、y、z是两两不等的实数，且满足下列等式：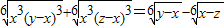
，则代数式x3+y3+z3-3xyz的值是（ ）A．0
B．1
C．3
D．条件不足，无法计算
【答案】分析：首先根据六次方根的被开方数为非负数与x、y、z是两两不等的实数，可得：
，
即可求得：x为0，y与z互为相反数，则可求得x3+y3+z3-3xyz的值．
解答：解：根据已知得：
，
∴x=0，
∴
=
-
=0，
∴y=-z，
∴x3+y3+z3-3xyz=0+y3-y3-0=0．
故选A．
点评：此题考查了六次方根的被开方数是非负数的性质与不等式组解集的求解方法．此题比较难，注意仔细分析．
，即可求得：x为0，y与z互为相反数，则可求得x3+y3+z3-3xyz的值．
解答：解：根据已知得：
，∴x=0，
∴
=-=0，∴y=-z，
∴x3+y3+z3-3xyz=0+y3-y3-0=0．
故选A．
点评：此题考查了六次方根的被开方数是非负数的性质与不等式组解集的求解方法．此题比较难，注意仔细分析．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
阅读下面的短文，并解答下列问题：
程
2011年4月28日，以“天人长安，创意自然一一城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园，这次园艺会的门票分为个人票和团体票两大类，其中个人票设置有三种：
某社区居委会为奖励“和谐家庭”，欲购买个人票100张，其中B种票的张数是A种票张数的3倍还多8张，设购买A种票张数为x，C种票张数为y
（1）写出y与x之间的函数关系式；
（2）设购票总费用为W元，求出w（元）与x（张）之间的函数关系式；
（3）若每种票至少购买1张，其中购买A种票不少于20张，则有几种购票方案？并求出购票总费用最少时，购买A，B，C三种票的张数．
| 票的种类 | 夜票（A） | 平日普通票（B） | 指定日普通票（C） |
| 单价（元/张） | 60 | 100 | 150 |
（1）写出y与x之间的函数关系式；
（2）设购票总费用为W元，求出w（元）与x（张）之间的函数关系式；
（3）若每种票至少购买1张，其中购买A种票不少于20张，则有几种购票方案？并求出购票总费用最少时，购买A，B，C三种票的张数．