题目内容
20.已知坐标系中两点A(0,4),B(8,2),点P是x轴上的一点,求PA+PB的最小值10.分析 根据“两点之间,线段最短”来解答问题:作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P,即点A、P、B′共线时,PA+PB的值最小.
解答 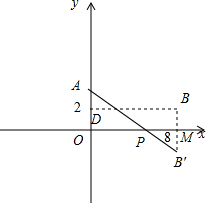 解:如图,作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P.
解:如图,作出点B关于x轴的对称点B′,过B′作B′M⊥x轴,M是垂足,连结AB′,交x轴于点P.
∵点B关于x轴的对称点是B′,∴PB=PB′,
∴AB′=AP+PB′=AP+PB,
而A、B′两点间线段最短,
∴AB′最短,(两点之间,线段最短),即AP+PB最小,
∴在Rt△AMB′中,AM=3,MB′=8,
∴AB′=10.
即PA+PB的最小值为10.
故答案是:10.
点评 此题主要考查了轴对称最短路线问题,求两线段之和最小的基本方法是作其中一个已知点关于直线的对称点,从而将两条线段之和转化为另一个已知点与对称点之间的线段.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
15.平行四边形的两条对角线分别为4和6,则其中一条边x的取值范围为( )
| A. | 2<x<3 | B. | 1<x<5 | C. | 0<x<4 | D. | 0<x<6 |
10.下列事件中,是必然事件的是( )
| A. | 明天一定会下雨 | B. | 购买一张彩票,中奖 | ||
| C. | 抛出的篮球会下落 | D. | 坐公交车有位子 |