题目内容
1.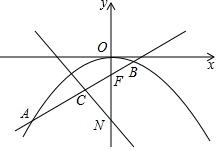 如图,过F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-$\frac{1}{4}$x2交于A(x1,y1),B(x2,y2)两点.
如图,过F(0,-1)的直线y=kx+b(k≠0)与抛物线y=-$\frac{1}{4}$x2交于A(x1,y1),B(x2,y2)两点.(1)求b值;
(2)求x1x2的值;
(3)若线段AB的垂直平分线交y轴于N(0,n),求n的取值范围.
分析 (1)根据题意即可得到结论;
(2)根据一元二次方程根与系数的关系即可得到结论;
(3)由(2)得,x1+x2=-$\frac{-k}{-\frac{1}{4}}$=-4k,求得xC=$\frac{{x}_{1}+{x}_{2}}{2}$=-2k,yC=-2k•k-1=-2k2-1,根据CN⊥AB,得到kCN=-$\frac{1}{k}$,求得直线yCN=-$\frac{1}{k}$(x+2k)-2k2-1,于是得到结论.
解答 解:(1)∵直线y=kx+b过F(0,-1),
∴b=-1;
(2)∵b=-1,
∴直线的解析式为:y=kx-1,
解$\left\{\begin{array}{l}{y=kx-1}\\{y=-\frac{1}{4}{x}^{2}}\end{array}\right.$得-$\frac{1}{4}$x2-kx+1=0,
∴x1x2=$\frac{1}{-\frac{1}{4}}$=-4;
(3)由(2)得,x1+x2=-$\frac{-k}{-\frac{1}{4}}$=-4k,
∴xC=$\frac{{x}_{1}+{x}_{2}}{2}$=-2k,yC=-2k•k-1=-2k2-1,
∵CN⊥AB,
∴kCN=-$\frac{1}{k}$,
∴yCN=-$\frac{1}{k}$(x+2k)-2k2-1,
当x=0时,n=-2-2k2-1=-2k2-3,
∵k≠0,
∴n<-3.
点评 本题考查了二次函数的性质,求函数的解析式,二元一次方程根与系数的关系,正确理解题意是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若一个角等于它余角的2倍,则这个角是( )度.
| A. | 75 | B. | 60 | C. | 15 | D. | 30 |
9.若方程5x=3+2a与方程2x+5=7的解相同,则a=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
6.黄冈农科院培育的“黄金8号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
(Ⅰ)根据题意,填写下表:
| 购买种子的数量/kg | 1.5 | 2 | 3.5 | 4 | … |
| 付款金额/元 | 7.5 | 10 | 16 | 8 | … |
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
13.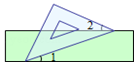 将含有45°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=15°,则∠2的度数为( )
将含有45°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=15°,则∠2的度数为( )
 将含有45°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=15°,则∠2的度数为( )
将含有45°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=15°,则∠2的度数为( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
 已知平行四边形ABCD的对角线相交于点O,且AC=12,BD=8,BC=5,则△AOD的周长=15.
已知平行四边形ABCD的对角线相交于点O,且AC=12,BD=8,BC=5,则△AOD的周长=15. 如图,矩形ABCD,AB=1,BC=2,点O为BC中点,弧AD的圆心为O,则阴影部分面积为$\frac{π}{2}$.
如图,矩形ABCD,AB=1,BC=2,点O为BC中点,弧AD的圆心为O,则阴影部分面积为$\frac{π}{2}$.