Question

某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料．生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种材料各3千克．经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元．

（1）甲、乙两种材料每千克分别是多少元？

（2）现工厂用于购买甲、乙两种材料的资金不能超过10000元，且生产B产品要超过38件，问有哪几种符合条件的生产方案？

（3）在（2）的条件下，若生产一件A产品需加工费40元，若生产一件B产品需加工费50元，应选择哪种生产方案，才能使生产这批产品的成本最低？请直接写出方案．

Answer 1

【考点】一次函数的应用；二元一次方程组的应用；一元一次不等式组的应用．

【分析】（1）设甲种材料每千克x元，乙种材料每千克y元，根据题意列出方程，解方程即可；

（2）设生产B产品a件，生产A产品（60﹣a）件．根据题意得出一元一次不等式组，解不等式组即可得出结果；

（3）设生产成本为W元，根据题意得出W是a的一次函数，即可得出结果．

【解答】解：（1）设甲种材料每千克x元，乙种材料每千克y元，

依题意得：，

解得：；

答：甲种材料每千克25元，乙种材料每千克35元．

（2）设生产B产品a件，生产A产品（60﹣a）件．

依题意得：，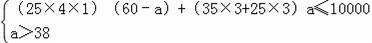

解得：38＜a≤；

∵a的值为非负整数，

∴a=39、40、41、42；

答：共有如下四种方案：

A（件）	21	20	19	18
B（件）	39	40	41	42

（3）生产A产品21件，B产品39件成本最低．理由如下：

设生产成本为W元，则W与a的关系式为：

W=（25×4+35×1+40）（60﹣a）+（35×3+25×3+50）a=55a+10 500，

即W是a的一次函数，

∵k=55＞0

∴W随a增大而增大

∴当a=39时，总成本最低；

即生产A产品21件，B产品39件成本最低．

【点评】本题考查了二元一次方程组的应用、一元一次不等式组的应用、一次函数的应用；根据题意中的数量关系列出方程组、不等式组、一次函数关系式是解决问题的关键．