题目内容
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 .
【答案】分析:连接DF、OE,过点D作DG⊥AC于点G,先证明四边形CGDF是矩形,得出DG=CF=y;再证明△AOE∽△ADG,根据相似三角形的性质即可求出答案.
解答: 解:连接DF、OE,过点D作DG⊥AC于点G.
解:连接DF、OE,过点D作DG⊥AC于点G.
∵∠C=∠CGD=∠CFD=90°,
∴四边形CGDF是矩形,
∴DG=CF=y;
∵OE∥DG,
∴△AOE∽△ADG,
∴ =
= ,
,
即 =
= ,
,
化简可得y= .
.
点评:主要考查了函数的定义和结合几何图形列函数关系式.
函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
解答:
 解:连接DF、OE,过点D作DG⊥AC于点G.
解:连接DF、OE,过点D作DG⊥AC于点G.∵∠C=∠CGD=∠CFD=90°,
∴四边形CGDF是矩形,
∴DG=CF=y;
∵OE∥DG,
∴△AOE∽△ADG,
∴
 =
= ,
,即
 =
= ,
,化简可得y=
 .
.点评:主要考查了函数的定义和结合几何图形列函数关系式.
函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.

练习册系列答案
相关题目
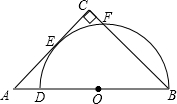 2,AD=1,则CF=
2,AD=1,则CF= 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 于点F.
于点F.