题目内容
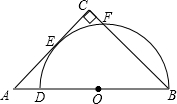（2013•山西模拟）如图，DB为半圆的直径，A为BD延长线上一点，AC切半圆于点E，BC⊥AC于点C，交半圆于点F．已知BD=4，AD=1，则CF=| 2 |
| 3 |
| 2 |
| 3 |
分析：首先利用三角形相似的判定方法证明△AEO∽△OMB，进而求出CE与BC的长，再利用切割线定理求出CF即可．
解答：解：连接OE，做OM⊥BC，
∵BC⊥AC，OM⊥BC，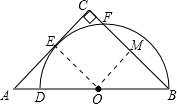
OM∥AC，
∴∠A=∠MOB，
∴∠AEO=∠OMB，
∴△AEO∽△OMB，
∴
=
，
∵OD=
BD=2，
∴A0=AD+OD=3，
∴AE=
=
，
解得：OM=
，
∴CM=OE=2，OM=CE=
，
∴BM=
，
∴BC=BM+CM=2+
=
，
∵CE2=CF×BC，
解得：CF=
．
故答案为：
．
∵BC⊥AC，OM⊥BC，
OM∥AC，
∴∠A=∠MOB，
∴∠AEO=∠OMB，
∴△AEO∽△OMB，
∴
| AE |
| OM |
| AO |
| BO |
∵OD=
| 1 |
| 2 |
∴A0=AD+OD=3，
∴AE=
| OA2-OE2 |
| 5 |
解得：OM=
2
| ||
| 3 |
∴CM=OE=2，OM=CE=
2
| ||
| 3 |
∴BM=
| 4 |
| 3 |
∴BC=BM+CM=2+
| 4 |
| 3 |
| 10 |
| 3 |
∵CE2=CF×BC，
解得：CF=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：此题主要考查了切线的性质定理、垂径定理以及相似三角形的性质定理与判定定理，求出BC与CE的长是解决问题的关键．
练习册系列答案
相关题目
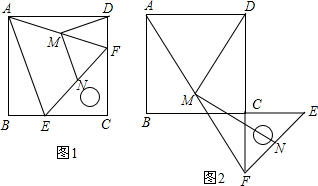（2013•山西模拟）操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．