Question

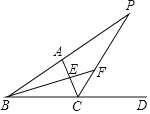
【题目】如图，已知BE是△ABC的角平分线，CP是△ABC的外角∠ACD的平分线．延长BE，BA分别交CP于点F，P．

（1）求证：∠BFC∠BAC；

（2）小智同学探究后提出等式：∠BAC=∠ABC+∠P．请通过推理演算判断“小智发现”是否正确？

（3）若2∠BEC﹣∠P=180°，求∠ACB的度数．

Answer 1

【答案】（1）证明见解析；（2）“小智发现”是错误的，证明见解析；（3）∠ACB=60°．

【解析】

（1）根据角平分线的定义得到∠PCD＝∠ACD，∠FBC＝∠ABC，根据三角形的外角的性质即可证明结论；

（2）根据（1）中的结论变形后可得结论；

（3）根据三角形的外角和角平分线的定义，综合已知，等量代换可得结论．

（1）∵CP是∠ACD的平分线，

∴∠PCD∠ACD．

∵BF是∠ABC的平分线，

∴∠FBC∠ABC，

∴∠BFC=∠PCD﹣∠FBC(∠ACD﹣∠ABC)∠BAC；

（2）由（1）知∠BFC∠BAC，

∴∠BAC=2∠BFC=2×(∠ABC+∠P)=∠ABC+2∠P，

∴“小智发现”是错误的；

（3）△ABE中，∠BEC=∠ABE+∠BAC∠ABC+∠BAC，

△ACP中，∠BAC=∠ACP+∠P，

∴∠BEC∠ABC+∠ACP+∠P∠ABC+∠PCD+∠P．

∵∠PCD∠ABC+∠BFC，

∴∠BEC∠ABC+∠P∠ABC∠BAC=∠ABC+∠P∠BAC．

∵2∠BEC﹣∠P=180°，

∴∠BEC∠P=90°，

∴90°∠P=∠ABC+∠P∠BAC，

　180°+∠P=2∠ABC+2∠P+∠BAC，

　180°=∠ABC+∠P+180°﹣∠ACB，

∠ACB=∠ABC+∠P=∠PCD=∠ACP，

∴∠ACB=60°．